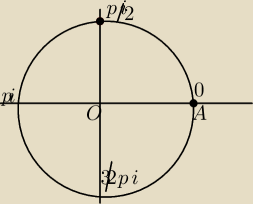
 Rozpatrujemy okrag jednostkowy (1 cwiartke .
Przedzial liczbowy 0≤α≤π/2 przedstawi się w postaci 1 ćwiartki
Przedzialowi domknietemu π/2≤α≤π odpowiada druga cwiartka
Oczywiście mogą tez być przedzialy otwarte
Każdy przedzial liczbowy 2kπ<α<(2k+0,5)π gdzie k (dowowlna liczba calkowita ma na okręgu
jednostkowym obraz w postaci pierwszsej ćwiartki otqwartej
Przedzial otwarty (2k+0,5)π<α<(2k+1)π ma obraz druga cwiartke otwarta
Moglby ktoś to dokładnie wytlumaczyc i dalej z tymi cwairtkami ?
Rozpatrujemy okrag jednostkowy (1 cwiartke .
Przedzial liczbowy 0≤α≤π/2 przedstawi się w postaci 1 ćwiartki
Przedzialowi domknietemu π/2≤α≤π odpowiada druga cwiartka
Oczywiście mogą tez być przedzialy otwarte
Każdy przedzial liczbowy 2kπ<α<(2k+0,5)π gdzie k (dowowlna liczba calkowita ma na okręgu
jednostkowym obraz w postaci pierwszsej ćwiartki otqwartej
Przedzial otwarty (2k+0,5)π<α<(2k+1)π ma obraz druga cwiartke otwarta
Moglby ktoś to dokładnie wytlumaczyc i dalej z tymi cwairtkami ?

 Wypilem dzisiaj jedna z pieprzem
Wypilem dzisiaj jedna z pieprzem 

 Już teraz mogę isc spac
Już teraz mogę isc spac
 Zadanie nie jest dziwne tylko pewnie może ja dziwnie to napisałem
Otoz mamy takie ćwiartki (chociaż teraz nie ma ćwiartek tylko 200ml )
1 0≤α≤π/2
2. π/2≤α≤π
3. π≤α≤1,5π
4 1,5π≤α≤2π
czyli wykonaliśmy jeden pelny obrot o 2π
Teraz wykonujemy następny obrot
1cwiartka będzie 2π≤α≤2,5π
2 cwiartka będzie 2,5π≤α≤3π
3 cwiartka będzie 3π≤α≤ 3,5π
4 cwiartka będzie 3,5π≤α≤4π czyli wykonaliśmy znowu jeden pelny obrot
i teraz 3 obrot
czyli
1 cwiartka 4π≤α≤4,5π
2 cwiartka 4,5π≤α≤5π
itd.
Oczywiście te przedzialy nie musza być domknięte −mogą być otwarte
Terraz chodzi mi o to jak te przedzialy zapisac ogolnie żeby był ogolny wzor na to
Potrzebne będzie mi to do rownan ale przedtem tez do określenia nierownosci w poszcegplnych
cwairtkach .
Potem to napiszse i będę prosil o wyjaśnienie
Zadanie nie jest dziwne tylko pewnie może ja dziwnie to napisałem
Otoz mamy takie ćwiartki (chociaż teraz nie ma ćwiartek tylko 200ml )
1 0≤α≤π/2
2. π/2≤α≤π
3. π≤α≤1,5π
4 1,5π≤α≤2π
czyli wykonaliśmy jeden pelny obrot o 2π
Teraz wykonujemy następny obrot
1cwiartka będzie 2π≤α≤2,5π
2 cwiartka będzie 2,5π≤α≤3π
3 cwiartka będzie 3π≤α≤ 3,5π
4 cwiartka będzie 3,5π≤α≤4π czyli wykonaliśmy znowu jeden pelny obrot
i teraz 3 obrot
czyli
1 cwiartka 4π≤α≤4,5π
2 cwiartka 4,5π≤α≤5π
itd.
Oczywiście te przedzialy nie musza być domknięte −mogą być otwarte
Terraz chodzi mi o to jak te przedzialy zapisac ogolnie żeby był ogolny wzor na to
Potrzebne będzie mi to do rownan ale przedtem tez do określenia nierownosci w poszcegplnych
cwairtkach .
Potem to napiszse i będę prosil o wyjaśnienie
| π | ||
0+2kπ<α< | +2kπ, k∊C | |
| 2 |
| π | |
+2kπ<α< π+2kπ | |
| 2 |
| 3 | ||
π+2kπ<α | π+2kπ | |
| 2 |
| 3 | |
π+2kπ<α<2π+2kπ | |
| 2 |
