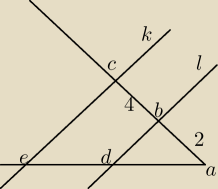
tales wd410: Proste k i l są równoległe. Długości odcinków |AB|, |BD| i |CE| są kolejnymi wyrazami ciągu arytmetycznego. Odcinek |BD| jest równy...

wd410:

cosinusx: Sprawdź, czy na pewno dobrze przepisałeś(aś) zadanie, bo wynik wychodzi ujemny, a nie może taki być.

utem: |AB|=2 |BD|=2+r, 2+r>0 |CE|=2+2r

AB		AC
	=		⇔
BD		CE

2		2+4
	=
2+r		2+2r

Dalej sam.

wd410: Cosinusx, mi też niestety wychodził wynik ujemny. Utem, tutaj też wychodzi r ujemne.

utem: No i co z tego, ma być spełniony warunek: 2+r>0 i jest. Czy odcinek BD nie może być mniejszy od 2?

wd410: Mi wychodzi r = −4 BD = 2 + r = 2 − 4 = − 2

utem: Za chwilę.

utem: To zadanie z testu wyboru? Jaką masz prawidłową odpowiedź? Bo szukam błędu w treści. Może wróćmy jutro do zadania, bo zasypiam

cosinusx: Wychodzi że BD=−2 a długość odcinka musi być >0.

utem: Wg danych podanych na rysunku, zadanie nie ma rozwiązania. Jakiś błąd w druku w treści zadania.