wyznacz przedziały monotoniczności i ekstrema funkcji Krzysiek: poproszę kogoś o sprawdzenie zadanie wyznacz przedziały monotoniczności i ekstrema funkcji wrzucam zdjęcie bo gdybym przepisał to, sam mętlik by się zrobił będę bardzo wdzięczny za pomoc http://postimg.org/image/cppadnuzd/

Krzysiek: brakuje jeszcze jednego założenia do dziedziny teraz zauważyłem

Krzysiek: ono i tak nie chyba nie zmienia rozwiązania, sam nie wiem .. proszę o opinię

Krzysiek: brak ekstremum

Krzysiek:

cosinusx: Dziedzina: 1−x>0 => 1>x ln(1−x)≠0 => 1−x≠1 ⇒ x≠0 D: x∊(−nieskończoność; 0)U(0,1)

cosinusx: Natomiast w 3) się pomyliłeś przy porównywaniu pochodnej do zera− w liczniku nie przepisałeś jedynki, a ona zmienia wynik

Krzysiek: juz poprawiam

Krzysiek: poprawiłem i z tego wyszło że funkcja osiąga maximum w punkcie (1−e, −e) w punkcie 3) wyszło x = 1 − e

misiak: taki zapis odpowiedzi budzi moje zastrzeżenia wg mnie powinniśmy zapisać: funkcja osiąga maximum lokalne, równe −e dla x=1−e . albo: f_max(1−e)=−e

Krzysiek: dobrze takiego zapisu będę się trzymał jak mi proponujesz zaczynam następne zadanie i wychodzi mi głupi punkt przegięcia nie pomyliłem się gdzies http://s1.postimg.org/4kxfydyrz/20160105_233306.jpg

misiak: przy drugiej pochodnej w liczniku −3x+2xlnx i nie skracaj....łatwiej uzasadniać zmianę znaku ..albo przypomnij, że x>0 dla x∊D

cosinusx: Wg mnie jest ok

cosinusx: Skoro założył, że x≠0, to może przez x skrócić, czyli podzielić.

misiak: y">0 ⇔ −3+lnx>0 ⇔lnx>3 ⇔ x>e³

Krzysiek: patrzę na pochodną i wydaje mi się ok jak w końcu jest

misiak: do poprawkiowinno być u mnie: −3+2lnx>0

misiak: to co zapisałeś w liczniku w ostatnim ułamku y" ? pozostałe zapisy do przyjęcia ..choć ciekawi mnie skąd taki wykres?

misiak:

	−3+2lnx
y"=
	x3

Krzysiek: z tą pochodną y'' to taki problem jest że tam nawiasy są i trzeba się ich trzymać myli mi się to jakoś inaczej robię teraz i mam w liczniku −3x +2xlnx

Krzysiek: w ostatnim ułamku zapisałem −1−2(1−lnx)

Krzysiek: czyli że dobrze mamy tą pochodną od początku

misiak: a wykres jest dobry? dla x>e^1,5 druga pochodna jest ujemna? u mnie wychodzi dodatnia

Krzysiek: teraz jak patrzę to chyba powinno być na odwrót na wykresie ujemna dodatnia

misiak: też tak myślę....nie wiem skąd u ciebie takie wykresy (trochę jak dla wielomianów) ja rozwiązuję nierówności logarytmiczne

Krzysiek: a pokaż jeśli możesz jak robisz tego typu zadania, może być zdjęcie, nawet lepiej

misiak: https://matematykaszkolna.pl/strona/1703.html

Krzysiek: nie wiem, przydała by się opinia jeszcze kogoś czy tak można jak ja robię

misiak: jeśli tak uczyliście się to pewnie tak.....tylko trzeba dobrze szkicować te wykresy... przedział − z dziedziny − jest ok potem do tego wykres....

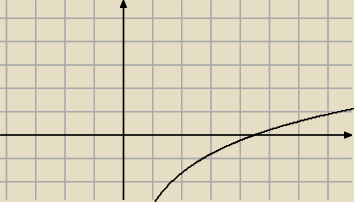
misiak: mamy narysować wykres znaków dla 2lnx−3

Krzysiek: wiesz misiak uczę się sam z tego co znajdę w sieci, a te wykresu u mnie to są tylko żeby kapować się jak idzie funkcja, do określenia monotoniczności wypukłości itp

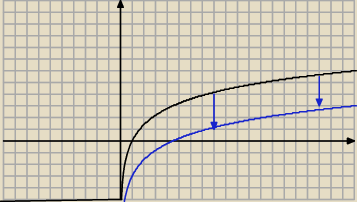
misiak: wykres funkcji y=2lnx oraz przesunięty 3 jednostki w dół : y=−3+2lnx

Krzysiek: rozumiem dzięki