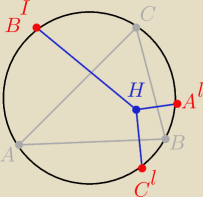
geometria geo.metria: niech trójkat ABC będzie trójkątem ostrokątym, a H punktem leżacym wewnątrz niego. Wykaż, że jeśli obrazy S_prAB(H), S_prAC(H), S_prBC(H) leżą naokręgu opisanym na trójkącie ABC, to H jest ortocentrum trójkąta AB

anaisy: Rozumiem, że S_prAB(H) oznacza odbicie symetryczne H względem AB? Niech X będzie ortocentrum tego trójkąta. Łatwo policzyć na kątach, że ∡AXB=180[deg]−∡ACB=∡AC'B=∡AHB, czyli H leży na okręgu (AXB). Analogicznie pokazujemy, że H leży na okręgach (CXB) i (CXA). Wiadomo, że te trzy okręgi przecinają się w dokładnie jednym punkcie X, czyli punkty X i H pokrywają się.

Eta: http://www.deltami.edu.pl/temat/matematyka/geometria/planimetria/2013/04/15/2012-09-k25.pdf

geo.metria: a dlaczego katAXB=180−ACB?

anaisy: Mamy ∡XCA=∡XBA oraz ∡XCB=∡XAB, skąd ∡AXB=180[deg]−∡XAB−∡XBA=180[deg]−∡XCB−∡XCA= =180[deg]−∡ACB

geo.metria: ok juz rozumiem ... ∡ACB=∡AC'B dlatego ze sa oparte na tym samym łuku? więc tam kontynuując Twój pierwszy komentarz nie powinno być czasem: AXB=180−ACB=180−AC'B ? i znowu tutaj nie wiem dlaczego to jest równe AHB

geo.metria: aha juz iwem − nie są oparte na tym samym łuku− tylko tak jak by na "przeciwnym" ...ale ze to równe AHB to dalej nie wiem

anaisy: Katy AHB i AC'B są równe ponieważ H i C' są symetryczne względem AB.