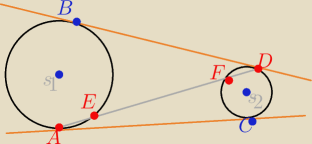
help geo.metria: dane są dwa okrędi O₁ i O₂ rozłączne zewnetrznie. Prste pr AC i pr BD sa ich wspólnymi stycznymi zewnetrznymi, przy czym A,C,B,D sa punktami styczności. odc AD przecina okręgi O1 i O2 odpowiednio w punktach E i F. wykaż, że |AE|=|FD|

Eta: Z tw. o stycznej i siecznej: |AC|²=|AD|*|AE| i |BD|²=|AD|*|DF|

|AC|2		|AE|
	=		oraz |AC|= |BD| .... ( dlaczego?....
|BD|2		|DF|

zatem |AE|= |DF| c.n.w

anaisy: Niech X, Y, Z będą środkami odpowiednio odcinków BD, AD, AC. Z tw. odwrotnego do tw. Talesa mamy, że Y leży na prostej XZ, która jest osią potęgową danych okręgów, stąd AY*YE=DY*YF. Ponieważ AY=YD, więc YE=YF, czyli AE=DF.

xoxo: a nie powinno byc czasem AC ²=AD*AF ? i BD²= DA*DE ? ii dlaczego AC=BD ?

geo.metria: ok juz wiem dlaczego ac=bd,

xoxo: dlaczego?

geo.metria: http://www.matmana6.pl/tablice_matematyczne/liceum/figury_plaskie_planimetria/102-styczne_i_sieczne tu jest

xoxo: dzieki juz rozumiem .... ale dalej nie wiem czemu |AC|²=|AD|*|AE| i |BD|²=|AD|*|DF| , a nie AC²=AD*AF i BD²= DA*DE

geo.metria: dlatego, że: af=ad−df, ed=ad−ae, wiemy ze af=ed i wystarzy tylko podłożyć o to chodziło?

Kacper: biorę

5-latek: Czesc Kacper Niedlugo będziesz musial chyba zmienić mieszkanie na wieksze jak tak wszystko będziesz brał

Kacper: No jak trzeba to trzeba