funkcjaa, Zuzanna123: Zadanie 1. Dana jest funkcja kwadratowa f(x) = ax² + bx + c. Wyznacz wszystkie wartości parametrów a, b, c, wiedząc, że funkcja f jest rosnąca w przedziale (–∞, –1〉 i malejąca w przedziale 〈–1, +∞), jednym z jej miejsc zerowych jest liczba (–3), a w przedziale 〈0, 2〉 największą wartością funkcji jest liczba 6. Zadanie 3. Rozpatrujemy trójkąty prostokątne o sumie przyprostokątnych równej 10. Wybierz trójkąt o największym polu i oblicz pole koła opisanego na tym trójkącie. Zadanie 4. (5 pkt) Podaj przykład równania dwukwadratowego ax⁴ + bx² + c = 0, które: a) nie ma rozwiązań, b) ma tylko dwa różne rozwiązania, c) ma tylko trzy różne rozwiązania. W każdym przypadku przeprowadź rozumowanie uzasadniające poprawność przykładu.

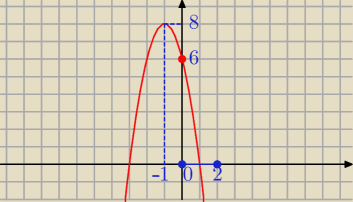
Janek191: z.1 p = − 1 x₁ = − 3 f(0) = 6 zatem f(x) = a*( x − p)² + q f(x) = a*( x + 1)² + q czyli f( − 3) = 0 ⇔ a*(− 3 + 1)² + q = 4 a + q = 0 f(0) = 6 ⇔ a*1² + q = a + q = 6 Mamy układ równań: 4a + q = 0 a + q = 6 −−−−−−−− odejmujemy stronami 3 a = − 6 a = − 2 ===== q = 6 − q = 6 + 2 = 8 Odp. f(x) = − 2*(x + 1)² + 8 = − 2*( x² + 2 x + 1) + 8 = − 2 x² − 4 x + 6 zatem a = − 2, b = − 4, c = 6 ================ Patrz też na wykres

Janek191: z.2 a,b,c − długości boków Δ prostokątnego oraz a < b < c Mamy a + b = 10 ⇒ b = 10 − a P = 0,5 a*b = 0,5 a*( 10 − a) = 5 a − 0,5 a² = − 0,5 a² + 5 a − 0,5 < 0 więc funkcja P(a) = −0,5 a² + 5 a osiąga maksimum dla

	− 5
a = p =		= 5
	2*(− 0,5)

Wtedy b = 10 − 5 = 5 Mamy Δ prostokątny równoramienny. c = a√2 = 5√2 r = 0,5 c = 2,5 √2 − promień okręgu opisanego na tym Δ.