funkcje kwadratowe Zuzanna123: Zadanie. 1 Określ liczbę rozwiązań równania f(x) = m w zależności od wartości parametru m (m ∈ R), jeśli f(x)= x² + 6x + 8, jeśli x nalezy (−nieskonczonosc, −2) −x²+4, jeśli x nalezy <−2, 2> x² − 6x + 8, jesli x nalezy (2, nieskonczonosc) a nastepnie podaj rozwiazanie nierownosci f(x+1)−4 jest większe równe 0 Zad. 2 Określ liczbę rozwiązań równania f(x) = m w zależności od wartości parametru m (m ∈ R), jeśli f(x)= x² + 6x + 8 jęsli x należy od (−nieskonczonosc, −2> x² − 4 jeśli x należy (−2, nieskonczonosc) Zadanie 3. Rozpatrujemy trójkąty prostokątne o sumie przyprostokątnych równej 10. Wybierz trójkąt o największym polu i oblicz pole koła opisanego na tym trójkącie. Zadanie 4. (5 pkt) Podaj przykład równania dwukwadratowego ax⁴+ bx² + c = 0, które: a) nie ma rozwiązań, b) ma tylko dwa różne rozwiązania, c) ma tylko trzy różne rozwiązania. W każdym przypadku przeprowadź rozumowanie uzasadniające poprawność przykładu.

Uu: A>0 f rosn ramiona w dol Czyli od −∞ do "q" 2 rozw pozniej dla q 1 rozw i od q do ∞ brak

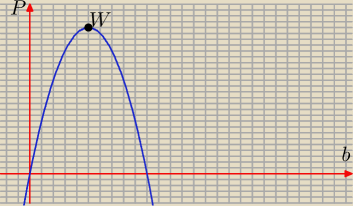
cosinusx: Zad.3 a+b=10 −> a=10−b

	ab
P=
	2

	(10−b)b
P(b)=		−pole jest funkcją zmiennej b
	2

U{(10−b)b}{2=0 (10−b)b=0 −b²+10b=0 −współczynnik przy b² to (−1), zatem ramiona paraboli będą skierowane w dół, czyli maksimum będzie w wierzchołku (W). W ma współrzędne (b₀,P_max). Nas interesuje wartość pola, czyli druga współrzędna− P_max Z funkcji kwadratowej: Δ=B²−4AC=100

	−Δ		−100
q=		=		=25
	4A		−4

Zatem maksymalne pole to 25.

cosinusx: Przepraszam, tam powinno być że 2P=25, zatem pole wynosi 12,5.

	(10−b)b
Bierze się to stąd, że było P(b)=		a ja później operowałam już tylko na (10−b)b,
	2

czyli dwukrotności pola, czyli 2P.

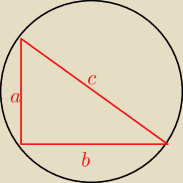
cosinusx: Obliczmy teraz dla jakiego b zachodzi taka wartość pola.

	−B		−10
b0=		=		=5
	2a		−2

b=5 a=10−b=5 Przeciwprostokątna trójkąta jest jednocześnie średnicą koła opisanego. Zatem c=2R. c²=a²+b²=25+25=50 c=5√2

	c		5√2
R=		=
	2		2

	50		25
P=πR2=π*		=		π=12,5π
	4		2