Taki mały smaczek Mateusz: W kule wpisano stożek . Wykaż ,że objetość stożka Vs , i objetosc kuli Vk spełniają warunek Vs≤8/27Vk Bardzo proszę o rozwiązanie bo te zadanie mnie pogrąża .

Mateusz: Ma ktoś jakiś pomysł ?

Godzio: Zaraz się okaże

Godzio:

	4
Vk =		πR3
	3

	1
Vs =		πr2H
	3

2R² − 2R²cos2α = l² l² = 2R²(1 − cos2α) l² = 2R²(1 − cos²α + sin²α) l² = 4R²sin²α l = 2Rsinα

	H
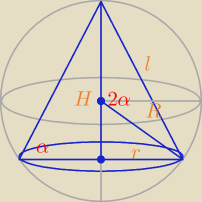
sinα =		⇒ H = lsinα = 2Rsin2α
	l

	r
cosα =		⇒ r = lcosα = 2Rsinαcosα
	l

	1		8
Vs =		π4R2sin2αcosα * 2Rsin2α =		πR3 * sin4α * cos2α
	3		3

	4		3
Vk =		πR3 ⇒ πR3 =		Vk − wstawiamy do Vs
	3		4

	3		8
Vs =		Vk *		* sin4α * cos2α = 2Vk * sin4α * cos2α
	4		3

Znajdźmy teraz maksimum funkcji f(α) = sin⁴α * cos²α = sin⁴α * (1 − sin²α) sin²α = t ∊ <0,1> g(t) = t²(1 − t) = − t³ + t²

	2
g'(t) = − 3t2 + 2t = 0 ⇒ t(−3t + 2) = 0 ⇒ t = 0 lub t =
	3

Sprawdzamy dla jakiej wartości osiągnięte jest maksimum g(1) = 0 g(0) = 0

	2		4		1		4
g(		) =		*		=		stąd
	3		9		3		27

	4
sin4α * cos2α ≤		, stąd
	27

	4		8
Vs = 2Vk * sin4α * cos2α ≤ 2Vk *		=		Vk
	27		27

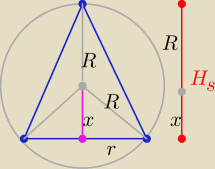Eta: Inny sposób ( bez trygonometrii x>0 H=R+x , r²= R²−x²

	π		π
V(st) =		(R2−x2)(R+x) =		(R+x)2(R−x)
	3		3

	π
V'(x)=		( 2(R+x)(R−x)−(R+x)2
	3

	R
V'(x)=0 ⇔ (R+x)(2R−2x−R−x)=0 ⇔ (R+x)(R−3x)=0 ⇒ x=
	3

	R		π		4R		2R		32πR3
V(st, max)(		)=		*(		)2*		=
	3		3		3		3		27

	4
V(kuli) =		πR3
	3

	R
( sprawdzić czy jest maximum dla x=		...........
	3

to

V(st,max)		8
	= .....
V(kuli max)		27

	8
zatem V(st) ≤		V(kuli)
	27

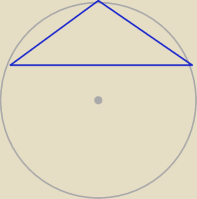Godzio: A co gdy mamy taką sytuację ? (chyba trzeba wtedy rozważać 2 przypadki?)

misiak: albo tak: R²=r²+(H−R)² r²=2HR−H²

	1
Vs=		πr2H
	3

	π
Vs=		(2HR−H2)H , 2R−H>0
	3

	π
Vs=		(2RH2−H3) , 0<H<2R
	3

	π
V's(H)=		(4RH−3H2)
	3

V'_s(H)=0 4RH−3H² =0

	4
H=0 lub H=		R
	3

	4		π		16		4
Vmax=V(		R)=		*		R2(2R−		R=
	3		3		9		3

	π		32		8		4		8
=		*		R3=		*		πR3=		Vk
	9		9		27		3		27

Eta:

Mateusz: Dzięki wielkie , wczoraj już sie podałem dzięki za każdą odpowiedz