Układy nierówności liniowych Paulina: Przedstaw ilustrację graficzną układu nierówności. Które z punktów P(6,1) Q(−3,5) R(8,−3) należą do otrzymanego zbioru. 2x+y+1≥0 x+2y−7<0

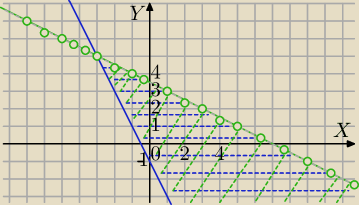
utem: y≥−2x−1 punkty nad prostą y=−2x−1 i na prostej

	1		7		1		7
y<−		x+		punkty poniżej prostej y=−		x+
	2		2		2		2

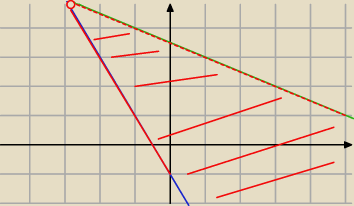
cosinusx: 2x+y+1≥0 x+2y−7<0 y≥−2x−1 2y<−x+7 y≥−2x−1 (niebieski wykres)

	1
y<−		x+3,5 (zielony wykres)
	2

Obszar spełniający układ równań, to ten zaznaczony na czerwono (tam gdzie było na zielono− linia przerywana, bo był znak <, tam gdzie na niebiesko− linia ciągła (aż do końca, ja zaznaczyłam fragment, żeby nie zakryć koloru niebieskiego), bo był znak ≥. Punkt przecięcia wykresów nie należy− puste kółko. Sprawdzenie punktów: P(6,1) −> x=6, y=1 2x+y+1≥0 (?) 12+1+1=14≥0 −pierwsze spełnione x+2y−7<0 (?) 6+2−7=1>0 −druga nierówność nie spełniona −> punkt P nie należy I tak dalej każdym punktem. Aby należał obie nierówności muszą być spełnione.