zanalizuj liczbe rozwiązań względem parametru k
w: Czy ktoś by mnie oświecił jak się do tego zabrać?
|x2+2x−3|=k|x+3|
4 sty 17:39
Paulina: Δ=4+12=16
k=|x−1|
rysujesz wykres funkcji
|f(x)| f(x)= x−1
wektor [1,0] f(x)=x
4 sty 17:43
utem:
Podpowiedź
Najpierw przedstaw trójmian w postaci iloczynu.
4 sty 17:46
utem:
Zał.
x≠−3
4 sty 17:47
w: Hm, a skąd bierze się 2 część z k=/x−1/ ?
4 sty 17:50
Godzio:
x = −3 jest rozwiązaniem niezależnie od k.
Podzielmy przez |x + 3| zakładając, że x ≠ − 3
|x − 1| = k
Dla k < 0 równanie nie ma rozwiązań. Dla k > 0 i k ≠ 4 (dlaczego?) ma dwa rozwiązania.
Dla k = 4 ma jedno rozwiązanie
Łącznie
Dla k < 0 mamy jedno rozwiązanie
Dla k > 0 i k ≠ 4 ma 3 rozwiązania
Dla k = 4 ma jedno rozwiązanie
4 sty 17:50
Paulina: 17.50 w
| | |(x+3)(x−1)| | |
stąd, że |
| skracasz i zostaje Ci |x−1| |
| | |x+3| | |
i jeszcze zał x≠−3
4 sty 17:54
w: Dziękuję dobrzy ludzie, jednak przerwa świąteczna wysysa z człowieka rozum

4 sty 18:00
Godzio:
Mała nieścisłość u Ciebie, dla k > 0 będą owszem dwa rozwiązania, ale trzeba na to uważać bo
dla k = 4 mamy x = −3, które już jest rozwiązaniem

Ja u siebie nie uwzględniłem k = 0.
Wtedy mamy dwa rozwiązania

4 sty 18:11
utem:
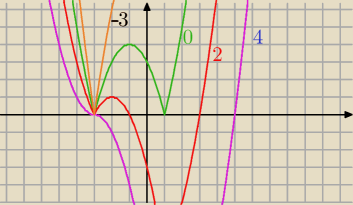 Paulino
Paulino, w tym zadaniu, znak w wyrażeniu |x+1| tylko wpłynął na jedną sytuację.
( to dla Ciebie mały problemik)
Godzio , masz rację. (z k=4)
Analiza:
|(x+3)*(x−1)|−k*|x+3|=0
|x+3|*(|x−1|−k)=0
x=−3 jest rozwiązaniem niezależnie od wyboru k, zatem w pewnej sytuacji może być pierwiastkiem
podwójnym.
lub
|x−1|=k
k=0 jedno rozwiązanie: x=1
k<0 brak rozwiązań
k>0 dwa rozwiązania , sprawdzamy jakie k otrzymamy dla x=−3,
|−3−1|=4 wtedy:
k=4
=====================================
łącznie:
1) k=0
(1+1=2 rozwiązania)
2) k>0 i k≠4
(1+2 =3 rozwiązania
3) k=4
1+1=2 rozwiązania
4) k<0 jedno rozwiązanie x=−3
===================
4 sty 18:59

 Ja u siebie nie uwzględniłem k = 0.
Wtedy mamy dwa rozwiązania
Ja u siebie nie uwzględniłem k = 0.
Wtedy mamy dwa rozwiązania
 Paulino, w tym zadaniu, znak w wyrażeniu |x+1| tylko wpłynął na jedną sytuację.
( to dla Ciebie mały problemik)
Godzio , masz rację. (z k=4)
Analiza:
|(x+3)*(x−1)|−k*|x+3|=0
|x+3|*(|x−1|−k)=0
x=−3 jest rozwiązaniem niezależnie od wyboru k, zatem w pewnej sytuacji może być pierwiastkiem
podwójnym.
lub
|x−1|=k
k=0 jedno rozwiązanie: x=1
k<0 brak rozwiązań
k>0 dwa rozwiązania , sprawdzamy jakie k otrzymamy dla x=−3,
|−3−1|=4 wtedy:
k=4
=====================================
łącznie:
1) k=0
(1+1=2 rozwiązania)
2) k>0 i k≠4
(1+2 =3 rozwiązania
3) k=4
1+1=2 rozwiązania
4) k<0 jedno rozwiązanie x=−3
===================
Paulino, w tym zadaniu, znak w wyrażeniu |x+1| tylko wpłynął na jedną sytuację.
( to dla Ciebie mały problemik)
Godzio , masz rację. (z k=4)
Analiza:
|(x+3)*(x−1)|−k*|x+3|=0
|x+3|*(|x−1|−k)=0
x=−3 jest rozwiązaniem niezależnie od wyboru k, zatem w pewnej sytuacji może być pierwiastkiem
podwójnym.
lub
|x−1|=k
k=0 jedno rozwiązanie: x=1
k<0 brak rozwiązań
k>0 dwa rozwiązania , sprawdzamy jakie k otrzymamy dla x=−3,
|−3−1|=4 wtedy:
k=4
=====================================
łącznie:
1) k=0
(1+1=2 rozwiązania)
2) k>0 i k≠4
(1+2 =3 rozwiązania
3) k=4
1+1=2 rozwiązania
4) k<0 jedno rozwiązanie x=−3
===================