planimetria Paulina: przekątne równoległoboku mają długość 10 i 26. Oblicz obwód równoległoboku, jeżeli jego pole jest równe 78. mam książkę nowej ery , a z tyłu odpowiedzi, i etapy jak należy ono rozwiązywać i nie rozumiem jednej rzeczy

	1		1
P=2*		* 5 *13 + 2 *		* 5 * 13sin(180−α)
	2		2

skad ten wzór na pole 5 i 13 to połowy przekątnych tego równoległoboku, a dalej nie rozumiem tego. skąd sie to wzieło i jaki jest wzór

Godzio:

	1
Wzór na pole trójkąta:		absinα gdzie α to kąt między bokami.
	2

Równoległobok jest podzielony na 4 trójkąty, po 2 takie same, przekątne przecinają się pod kątem α, kąt dopełniający to 180 − α. Pierwszy trójkąt ma wymiary 5 x 13 i kąt α, drugi 5 x 13 i kąt 180 − α Ponieważ są po dwa takie trójkąty to z przodu masz 2 *

Godzio: Znajomość wzorów to podstawa, bez nich nie wpadniesz na pomysł bo nie będziesz wiedzieć z czego możesz korzystać. Zacznij od nich i od prostych zadań z nich korzystających. W ten sposób łatwo się ich nauczysz. Przeleć sobie działy, które masz tutaj, a później pójdzie z górki.

Paulina: masz rację, znałam ten wzór, ale nie wiedziałam w jakim sensie jest użyte wyrażenie ab. stokrotne dzieki.

Paulina: sin(180 − α)=sinα (w drugiej sinus jest dodatni)

	1		1
P=2*		*5*13 sinα + 2*		*5*13sinα
	2		2

P=130sinα 130sinα=78

	3
sinα=
	5

a dalej to wiem już o co chodzi,, dzieki

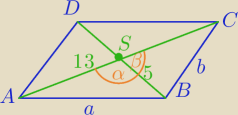
utem: α+β=180 β=180−α sin(180−α)=sinα

	1
PΔASB=		*13*5*sinα
	2

	1
P▱=4*		*13*5*sinα=10*13sinα
	2

10*13sinα=78 /:13

	6		3
sinα=		=
	10		5

Dalej dasz radę?