napisać równianie stycznej do krzywej Krzysiek: napisać równianie stycznej do krzywej to już jest dla mnie trudnee z samą pochodną mam problemy robię to tak ...

	1
y = (1 +		)ln1x w punkcie (1, y0) o co tu chodzi że w punkcie y0 ?
	x

	1
y ' = [(1 +		)ln1x ] ' =
	x

	1		1		1
= ln		(1 +		)ln1x − 1 * (1+		) ' =
	x		x		x

	1		1		1
= ln		(1 +		)ln1x − 1 * (−		)
	x		x		x2

po podstawieniu za x 1 wyszło że f ' (1) = 0 z czego całość była by y − y₀ = 0 y = y₀ nie mam pojęcia

Arturek_lat_7: y₀ oznacza wartosc funkcji dla danego x Innymi slowy −−− podstaw x=1 i wyznacz wartosc funkcji i masz y₀

Krzysiek: a no taak w takim razie wyszło by że końcowa odpowiedz dla całego zadania to y = 1 nadal nie wiem czy jest dobrze ale trzymam się tego co napisałem poproszę kogoś o sprawdzenie

Krzysiek:

Krzysiek:

Krzysiek:

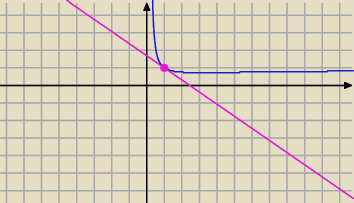
utem: y=f '(1)*x+b

	1
f(1)=(1+		)ln(1)=20=1 styczna przechodzi przez punkt(1,1)
	1

1=f '(1)*1+b Sprawdź pochodną: f '(1)=−ln(2) 1=−ln(2)+b b=1+ln(2) y=−ln(2)*x+1+ln(2) Przekształcam wzór funkcji: (łatwiej obliczyć pochodną)

	1		x+1		x
f(x)=(1+		)ln1−lnx=(		)−lnx=(		)ln(x)
	x		x		x+1

	x
f'(x)=[eln(x)*ln(		)]'=
	x+1

= policzysz, czy pomóc?

Krzysiek: męczę się z tą pochodną właśnie za nic nie mogę tego obliczyć tym moim sposobem ... strasznie dużo obliczeń

Krzysiek: dobrze wyszło mi też że f(1)' = − ln2 rozwiąże całe i zobaczysz jak możesz czy jest ok

Krzysiek: nie zauważyłem że rozwiązałeś tak samo mi wyszło teraz/ dziękuję bardzo

utem:

	x
f '(x)= elnx*ln(xx+1)*[lnx*ln(		)]'=
	x+1

	x		1		x+1		1*(x+1)−x*1
=(		)ln(x)*[		*ln(xx+1)+lnx*		*		]=
	x+1		x		x		(x+1)2

	x		1		x		1
=(		)ln(x)*[		*ln(		)+		*lnx]
	x+1		x		x+1		(x+1)

	1		1		1		1
f'(1)=		ln(1)*[		*ln(		)+		*ln1]=1*[ln(1)−ln(2)+0]=−ln(2)
	2		1		2		2

Krzysiek: