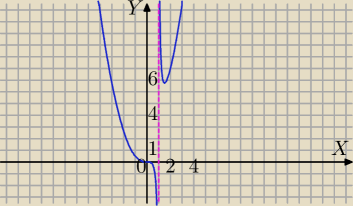
Badanie przebiegu zmiennosci funkcji Danielczyk: Prosze pomoc z tym zadaniem juz trzecia godzine nie moge znalesc prawidlowej odpowiedzi Zbadac przebieg zmiennosci funkcji i sporzadzic jej wykres: f(x)=x³/x−1

Ola: 1. Oblicz pochodną f(x) 2. Przyrównaj do zera 3. tam gdzie f'(x)>0 funkcja jest rosnąca, a tam gdzie f'x<0 funkcja jest malejąca f'(x)=0

Danielczyk: nie moge zrozumiec jak trzeba robic 3 punkt

5-latek: baju −baju Mysle ze sobie dopiero przypomniales ze masz na jutro zadanie . Badanie przebiegu zmiennosi funkcji zaczyna się od wyznaczenia dziedziny tego nawet nie potrafisz ?

Metis: No Ola streściła cały schemat badania przebiegu zmienności funkcji zawarła w III punktach

Eta: http://www.math.com.pl/analiza-matematyczna-1/badanie-przebiegu-zmiennosci-funkcji/

Danielczyk: Czy moze ktos normalnie wyjasnic jak to trzeba zrobic jestem troche glupym z wyzszej mathmy

Danielczyk: Dzieki

utem:

	x3
f(x)=
	x−1

1) dziedzina x−1≠0⇔x≠1 D=R\{1} 2) Granica na krańcach dziedziny:

	x3		x2
lim x→∞		=lim x→∞		=∞
	x−1		1   1−   x

	x3
lim x→−∞		=∞
	x−1

	x3
limx→1−		=−∞
	x−1

	x3
limx→1+		=∞
	x−1

3) x=1 asymptota pionowa 4) Monotoniczność i ekstrema

	3x2(x−1)−x3		3x3−3x2−x3
f'(x)=		=
	(x−1)2		(x−1)2

	2x3−3x2
f'(x)=
	(x−1)2

f'(x)=0⇔2x³−3x²=0⇔ x²*(2x−3)=0

	3
x=0 lub x=
	2

Znak pochodnej: f'(x)>0 i x≠1 x²*(2x−3)>0⇔

	3
2x−3>0⇔x>
	2

	3
Dla x>		funkcja rosnąca
	2

	3		3		27   8		27
Dla x=		minimum f(		)=		=
	2		2		3   −1 2		4

f(x) malejąca dla x∊(−∞, 1)

	3
f(x) malejąca dla x∊(1,		)
	2

W x=0 nie ma ekstremum,pierwsza pochodna nie zmienia znaku przy przejściu przez x=0. 4) x=0 punkt przegięcia

Metis: Czytelne http://i.imgur.com/Ka96JgD.png