Geo analityczna Hedonista: W trójkącie prostokątnym ABC(|kątABC|=90) dwa wierzchołki mają współrzędne A(4,−5) i C(−8,5). Wyznacz współrzędne wierzchołka B, wiedząc, że pole trójkąta ABC jest równe 61. −wyznaczam |AC|=√244=2√61 − równanie prostej przechodzącej przez AC 10x+12y+20=0

	61
−ze wzoru na pole podstawiam 2√61 i wyznaczam h=
	√61

Chcę podstawić do wzoru na odległość punktu od prostej, ale brakuje mi jednego równania. Pomoże ktoś?

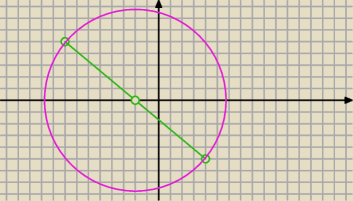
===: podpowiedź

Hedonista: No ideas

===: trzeci wierzchołek leży ma obwodzie okręgu

Hedonista: Z czego to wynika?

===: kąt oparty na średnicy

Hedonista: Okej czaję, wiem już ocb Tak z ciekawości, jak należałoby rozwiązać to zadanie w przypadku kiedy wysokość byłaby inna niż 1/2 AC

Tadeusz: policzyć wysokość ... rysować równoległe do AC odległe od niej o wysokość

utem: Wtedy np. tak: 1) piszesz równanie okręgu ośrodku S=(−2,0) i r=√61 2) piszesz równanie prostej równoległej do AC odległej od AC o podaną długość wysokości.( otrzymasz dwie proste) 3)Liczysz punkty przecięcia prostych z okręgiem.

Hedonista: thx