monotoniczność i ekstrema lokalne iga: Jak się zabrać za ten przykład? prosze o pomoc

	ex
f(x)=
	x

Janek191: 1) Dziedzina 2) I pochodna

iga: dochodze do pochodnej czyli:

ex*1+ex*x
x2

i co dalej?

iga: zamiast + ma być −

Janek191:

	ex*x − ex*1		ex ( x − 1)
f '(x) =		=
	x2		x2

Janek191: D = ℛ \ {0} e^x > 0 i x² > 0 więc kiedy pochodna jest ujemna, a kiedy dodatnia ?

iga: ujemna kiedy funkcja w przedziale maleje, a dodatnia gdy rośnie

Janek191: Podaj przedział, w którym f ' (x) < 0 ( wtedy f maleje), oraz przedział, w którym f ' (x) > 0 ( wtedy f rośnie ) .

iga: I z tym w tym przykładzie mam problem. f'(x)<0 dla x ( − nieskończoności do 0 ) f'(x)>0 dla x (0 do + nieskończoności)

Janek191: f '(x) < 0 ⇔ x − 1 < 0 ⇔ x < 0 ale x ≠ 0, więc f ' (x) < 0 gdy x ∊ ( − ∞; 0 ) ∪ ( 0 ; 1 )

Janek191: W I wierszu miało być .... ⇔ x < 1

Janek191: Zatem f maleje w przedziałach: ( − ∞ ; 0 ) , ( 0 ; 1)

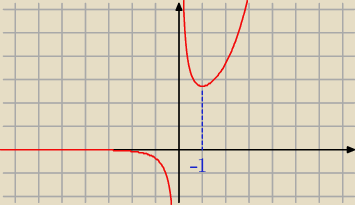
Janek191: Dla x > 1 jest f '(x) > 0 czyli dla x ∊ ( 1; +∞ ) funkcja f rośnie f'(x) = 0 ⇔ x = 1 i pochodna zmienia wtedy znak z − na + więc

	e1
f osiąga w x = 1 minimum lokalne ymin = f(1) =		= e
	1

Patrz na wykres

iga: już wszystko rozumiem, dziękuje baaardzo