Ktoś, coś ?? Ewaa: Dany jest równoległobok ABCD. Punkt E należy do boku AB, a punkt F do boku AD. Prosta EF przecina prostą CB w punkcie P, a prostą CD w punkcie Q. Wykaż, że pole trójkąta CEF jest równe polu trójkąta APQ.

Aga1.: Sprawdź treść zadania .

Ewaa: Na pewno jest taka. Zadanie pochodzi z I OMG

Kacper:

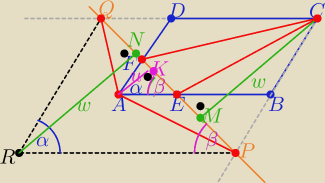
Eta: Ładne zadanko @ Aga1 ... treść jest poprawna Zaczynamy od rysunku Mamy wykazać,że P(CEF)= P(APQ) Budujemy równoległobok CPRQ i z własności równoległoboku ΔPCQ ≡ ΔPRQ zauważamy trójkąty podobne ΔAEF ∼ ΔPRQ z cechy (kkk)

	|PQ|
w skali k>0 , k=		⇒ |PQ|= k*|FE|
	|FE|

Również są proporcjonalne odpowiednie wysokości w=|NR|= | CM| −−− dł. wyskości ΔPRQ= dł wysokości ΔCEF u= |AK|−−−− dł. wysokości ΔAEF= dł. wysokości ΔAPQ

	w
to		=k ⇒ w=k*u
	u

	|PQ|*u		|FE|*k*u
P(APQ)=		=
	2		2

	|FE|*w		|FE|*k*u
P(CEF)=		=
	2		2

zatem P(ΔAPQ)= P(ΔCEF) c.n.w

Ewaa: DZIĘKUJĘ

Eta: