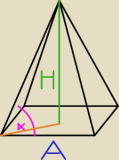
Objętość ostrosłupa Antek: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę α>45 (zobacz rysunek). Oblicz objętość tego ostrosłupa. Znalazłem kilka sposobów na rozwiązanie zadania, ale się zastanawiam, czy nie mogę po prostu policzyć pomarańczową krawędź jako a√2/2 a następnie H = (a√2*tgα)/2 i V=(a³√6tgα)/24

Antek: edit.. V=a²*1/3*H

dero2005: nie

Jack:

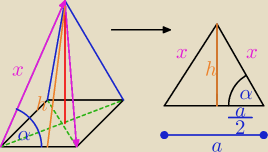
	a√2
pomarańczowa krawędź − prawda
	2

ale ten kąt alfa to jest między krawędzią boczną a podstawy czyli − patrz rysunek... x − krawedz boczna α = 45 stopni czy alfa jest wieksze od 45 stopni ?

Antek: a większe od 45 stopni czyli rozumiem, że mój błąd polega na tym, że alfa między krawędzią boczną a krawedzia podstawy to nie to samo co kąt między krawędzią boczną a przekątną podstawy?

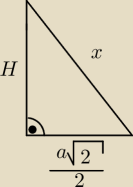
Jack: mozesz zrobic

	a   2
cos α =
	x

	0,5a
x =
	cos α

a potem z pitagorasa...(patrz trojkat)

Jack: tak, bo kat ktory zaznaczyles, to kat miedzy krawedzia boczna a plaszczyzna podstawy... jeszcze pewnie bedziesz mial katy miedzy plaszczyznami, dwuscienne i inne takie

Antek: nooooo.. Dzięki, o to mi chodziło