stereometria PILNE !! : Wspomóżcie mnie rozwiązaniem Z walca o średnicy 2m wycięto wpisany w niego graniastosłup prosty trójkątny. Miary dwóch kątów graniastosłupa są równe 45 stopni i 60 stopni, a przekątna ściany bocznej o najmniejszym polu jest nachylona do podstawy pod kątem 30 stopni. Oblicz ile papieru potrzeba zużyć by okleić wszystkie cztery bryły? PROSZĘ O POMOC

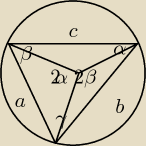
ula: podstawą jest Δ o kątach 45,60,75 z wzoru sinusów oblicz boki Δ

	a		a
R=		1=		→ a=√2
	2sinα		2sinα

	b
1=		→ b=√3
	2sin60

	c		√2+√6
1=		sin75=sin(30+45)=sin30cos45+cos30sin45=
	2sin75		4

	√2+√6
c=
	2

	√3+3
PΔ=uy{1}{2}*c*b*sin45=
	3

Wysokość wylicz z Δn, najkrótszy bok a, 30, H

	H		√6
tg30=		→ H=
	√2		3

Pole graniastosłupa

	√3+3
Pc=2Pp+Pb=2*		+H*a+Hb+Hc= wylicz podstaw boki i wusokość
	3

3 nasępne figury to wycinki walca Pwycinku= H*(pole wycinka koła podstawy − poleΔ)

	α
Pwycinka koła podstawy =		*πR2
	360

wycine oparty na boku a

	2*45
Pwycinka koła=		*π12=14π
	360

PΔ=¹₂R*R*sin90=¹₂ Pwycinka walca=H*(¹₄π−¹₂ podstaw tak samo zrób z wycinkami opartymi na b i c i wszystkie pola dodaj

ula: fajne zadanie tylko dużo pisania

ula: można to zrobić trochę prościej, nie wyliczać pól poszczególnych brył tylko uogólnic Pc=Pwalca+2Pścian bicznych graniastosłupa Pc=2πR²+2πRH+2aH+2bH+2cH

	√6		√6		√6		√2+√6		√6
Pc=2π+2π*		+2*√2*		+2*√3*		+2*		*
	3		3		3		2		3