Wysokość ostrosłupa trójkątnego matematyk97: Jak mogę obliczyć wysokość ostrosłupa trójkątnego, który ma w podstawie trójkąt równoramienny i znam długości wszystkich krawędzi? Spodek wysokości będzie leżeć na przecięciu symetralnych, więc to chyba nie stąd

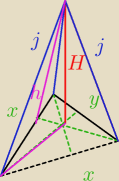
Jack: Mowisz ze co masz dane? : D

matematyk97: Długości wszystkich krawędzi tego ostrosłupa

matematyk97: A dlaczego ten różowy odcinek w podstawie ma długość h?

Jack: on nie ma dlugosci h... chcialem zbudowac trojkat ale... : D nie wyszlo... Znasz wszystkie krawędzie... i chcesz uzależnić H od krawędzi i podstawy tak ?

matematyk97: Muszę obliczyć objętość, więc muszę jakoś znaleźć H

Jack: bylbys w stanie dac dane...duzo latwiej sie liczy ; D a żadnego kąta nie masz podanego ?

matematyk97: Mam takie zadanko za 4pkt na maturę R. Trochę mi ciężko bo jeszcze nie miałem stereometrii W ostrosłupie trójkątnym ABCS o podstawie ABC i wierzchołku S dane są: |AB|=|AC|=26, |SB|=|SC|=2√194 i |BC|=2|AS|=20. Oblicz objętość tego ostrosłupa.

Mac: Aj, aj. Stereometra jest w 6 klasie szkoły podstawowej, a także w gimnazjum

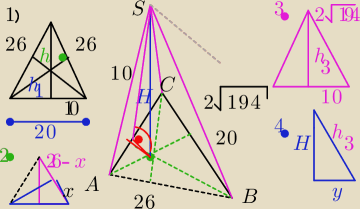
Jack: Z pierwszego trójkąta 1) − jest to trjkat w podstawie... 26² − 10² = h² h = 24 |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

	1
Pole trójkąta w podstawie :		* 20 * 24 = 240
	2

Wyraźmy te pole za pomocą h₁ , żeby je znaleźć

	1
240 = 26 *		* h1
	2

240 = 13 h₁

	240
h1 =
	13

Teraz pytanie...czy moge powiedziec ze ten trojkat (patrz drugi punkt) jest podobny do tego trójkąta jesli tak, to to duzo nam ulatwi... bo

24		240   13
	=
10		x

	100
stąd x =
	13

	100		238
a 26 − x wynosi −> 26 −		=
	13		13

chcialem stad ten igrek co na czwartym rysunku jest obczaic bo ten igrek to nic innego jak Ten fragment na rysnku głównym |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| trzeci rysunek ... h₃ − wysokosc sciany bocznej... znając h₃ −> czwarty rysunek z pitagorasa obliczamy H...

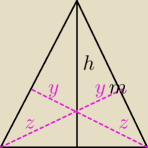
Jack: |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| Fragment w tej "klamrze" jest chyba bez sensu...dlatego go tak okreslilem...jedyne co jest nam niewiadome to podstawa jak sie przecina y + z = h₁....usimy znaleźć ten igrek ! : D

Jack: dobra...poddaje sie, pytaj pania Ete ktora rozwiaze wszystko ...

xyz: https://www.youtube.com/watch?v=U73LoXshp6o Podobne zadanie. Może pomóc

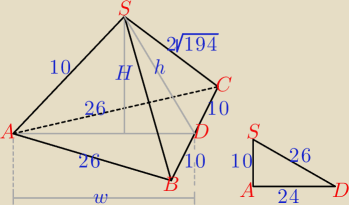
Bogdan: To kwestia ułożenia równań.. w = √26² − 10² = 24, h = √4*194 − 100 = 26 a więc trójkąt ADS o bokach długości 10, 24 i 26 jest przystający do trójkąta ADB i ADC i te trójkąty są prostokątne, stąd H = |AS| = 10

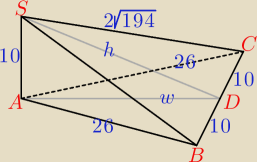
Bogdan: Tak wygląda ten ostrosłup

matematyk97: Dziękuję Bogdan i wszystko się zgadza Jak na to wpaść?

Bogdan: Ćwiczyć, ćwiczyć, ćwiczyć i bawić się tymi ćwiczeniami. Tu wystarczyło skorzystać z twierdzenia Pitagorasa, a więc zadanie dostępne dla gimnazjalisty.

Jack: a ja jak zawsz ... na około licze

Kacper: Zabieram