Zbiorem rozwiązań nierówności -1<x²+x<0 jest
Mateusz: Zbiorem rozwiązań nierówności −1<x²+x<0 jest :
a)R,
b)(−1;0),
c)(−∞;1),
d:(0;1)
Jak to rozwiązać?
2 sty 15:16
Jerzy:
⇔ x(x+1) < 0 i x(x+1) > −1
2 sty 15:17
Mateusz: no do tego doszedłem lecz nie mogę zrozumieć nierówności x(x+1) > −1 jak to narysować?
2 sty 15:19
Jerzy:
x2 + x + 1 > 0 ... policz :Δ
2 sty 15:20
Mateusz: Delta jest ujemna i brak miejsc zerowych, więc?
2 sty 15:20
Jerzy:
jest zawsze dodatnie, a więc większe od − 1
2 sty 15:21
Mateusz: Nie bardzo mogę to sobie wyobrazić, czyli jeżeli brak miejsc zerowych a jest dodatni i większy
od −1 to parabola jest nad osią x i się nie styka czyli powinno być liczby R do tego przypadku
tak?
2 sty 15:23
Mateusz: proszę o pomoc.
2 sty 15:33
Jerzy:
jedyny warunek to: x(x+1) < 0
2 sty 15:47
Mateusz: a ten drugi warunek? To jeżeli on jest większy od −1 to tak jakby przechodził przez miejsca
zerowe? A że delta jest ujemna nie ma miejsc zerowych to jest to niezgodne?
2 sty 16:01
Jerzy:
rozwiąż powyższą nieròwność i koniec zadania
2 sty 16:24
Jack:
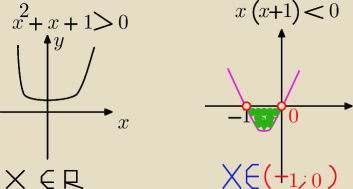
Część wspólna...
2 sty 16:38
Mateusz: ok! Dzięki wielkie.
2 sty 16:39
Jack: 
2 sty 16:42
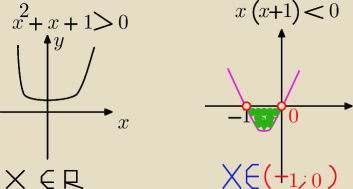 Część wspólna...
Część wspólna...
