Funkcja kwadratowa anka1342: Liczba 0 jest miejscem zerowym funkcji kwadratowej f(x)= 1−a+x−x² Oblicz a. Dla wyznaczonej wartości a naszkicuj wykres funkcji f Wyznacz argumenty dla których funkcja f przyjmuje wartości nieujemne

zeesp: Liczba 0 jest miejscem zerowym funckji kwadratowej f oznacza, że f(0)=0. Podstaw x=0 i przyrónaj do 0..

5-latek: To teraz napisz jaka jest definicja miejsca zerowego funkcji

anka1342: Miejsce zerowe funkcji − to taki argument x dla którego funkcja przyjmuje wartość 0 ale dalej nic z tego nie rozumiem...

anka1342: Jeżeli a=1 to parabole jest skierowana do góry ale gdzie na osi powinnam zaznaczyć a?

5-latek: To znaczy ze punkt ten ma wspolrzedne (x,0) Z warunków zadania wiemy ze nasze x=0 wiec ten punkt będzie mia wspolrzedne (0,0) Co jeszcze weimy Wiemy to ze ten punkt należy do wykresu tej funkcji NO a jeśli należy to spelnia równanie tej funkcji f(x) inaczej można zapisac jako y wiec y=1−a+x−x² Wstaw teraz wspolrzede tego punktu do tego równania i wylicz a

utem: f(0)=0

5-latek: Dobry wieczor Pozdrawiam

anka1342: podstawiając mam wzór 0=1−a+0−0² co idąc dalej daje mi a=1 ale nie wiem jak oznaczyć punkty na paraboli

Jerzy: musisz dziecko zrozumieć, co to jest funkcja

5-latek: Dobry wieczor J Wszystkiego dobrego Nowym Roku

5-latek: Teraz do wyjściowej funkcji wstaw a=1 i napisz wzor tej funkcji

anka1342: Tak powinien wyglądać wykres?

5-latek: Podstaw do wzoru za a =1 i napisz wzor funkcji Poza tym nie widzisz ze a<0 i ramiona będą w dol ?

anka1342: f(x)= 1−a+x−x² więc f(x)= 1−1+x−x² zostaje mi więc taka funkcja f(x)=−x²+x z tego wynika że a=−1 b=1 jeżeli x=0 to f(0)=0 faktycznie a<0 nie zauważyłam tego i co dalej? nic z tego nie rozumiem

5-latek: Tak naprawdę do rozwiązania tego zdania wystarczyla taka oto wiedza Jeśli mamy podane ze jedno z miejsc zerowych wynosi x=0 to wspolczynnik c musi wynosic 0 czyli c=0 jeśli mamy y=ax²+bx+c to c=0 gdyż wtedy mamy taka postac funkcji y=ax²+bx Teraz liczymy miejsca zerowe tej funkcji y=ax²+bx czyli ax²+bx=0 wyciamy x przed nawias i mamy

	−b
x(ax+b)=0 czyli x=0 lub ax+b=0 to ax=−b to x=
	a

wezmy nasza funkcje y=−x²+x Miejsca zerowe −x²+x=0 to x(−x+1)=0 to x=0 lub −x+1=0 to −x=−1 to x= ?

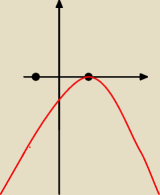
anka1342: czyli tak powinna wyglądać parabola x=1 a x to oś symetrii

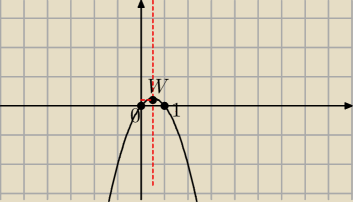
5-latek: Przeciez masz policzone miejsca zerowe Jedno wiesz ze wynosi x=0 bo masz podane w zadaniu Drugie wyliczylas ze wynosi x=1 Niech to będzie po waszemu czyli x₁=0 i x₂=1 Żeby naszkicować parabole trzeba mieć 3 charatertstyczne punkty Dwa już masz (miejsca zerowe ) Trzeci to wierzchołek Wsporzedna x_owa wierzchołka x_w=p= (albo skorzystasz ze wzorow

	x1+x2
albo wiesz ze xw=p=
	2

	1
czyli p=
	2

y_w=q=albo wzor albo q=f(p) g= x=−x²+x= −(0,5)²+0,5= −0,25+0,5=0,25

Jack: Co tu sie stalo Dlaczego tak? Jesli caly czas mowimy o funkcjo y = x − x² To tak jak napisal małolatek miejscami zerowymi (czyli tam gdzie twoj wykres przecina oś OX) Sa x = 0 oraz x = 1 W tych miejscach twoja parabola przecina oś...

anka1342: Dziękuję bardzo za pomoc i cierpliwość, postaram się nadrobić braki

5-latek: No i gitara

anka1342: Jeszcze w chcąc się upewnić argumenty dla których funkcja f przyjmuje wartości nieujemne x∈< 0,1> tak?

5-latek:

anka1342: Jeszcze raz dziękuję