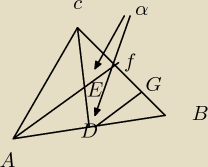 ja to zadanie też miałem w swoim zbiorze zadań... zaraz rozwiązanie napisze
ja to zadanie też miałem w swoim zbiorze zadań... zaraz rozwiązanie napisze  4.64
4.64  narysuj sobie środkową boku FB
|DG|=1/2|AF| i DG || FA => DG || FE
|AD| = |DB|
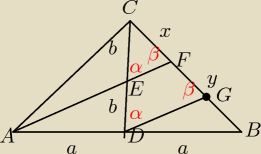
|CE| = |DE| = b
|FG| = |FB| = 1/2y (|FB|=y; |CF|=x)
ΔFEC jest przystający do ΔDGC (bkb − |CD| : |DG| = |CE| : |EF|)
narysuj sobie środkową boku FB
|DG|=1/2|AF| i DG || FA => DG || FE
|AD| = |DB|
|CE| = |DE| = b
|FG| = |FB| = 1/2y (|FB|=y; |CF|=x)
ΔFEC jest przystający do ΔDGC (bkb − |CD| : |DG| = |CE| : |EF|)
| x | b | ||
= | |||
| 1\2y+x | 2b |
| x | |
=1/2 | |
| y |
 i to się zgadza z odpowiedziami
i to się zgadza z odpowiedziami
| CF | x | ||
= | =?
| ||
| FB | y |
| 1 | ||
DG= | AF
| |
| 2 |
| 1 | b | |||
U{x}{U{x+ | y} = | |||
| 2 | 2b |
| 1 | ||
2x=x+ | y
| |
| 2 |
| 1 | ||
x= | y
| |
| 2 |
| x | 1 | ||
= | |||
| y | 2 |
 najpierw mi, teraz Tobie
najpierw mi, teraz Tobie 
| |CF| | CF | |||
ale tu przypadkiem nie wychodzi | zamiast | ? | ||
| FG | FB |