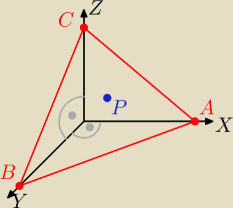
geometria analityczna Saizou : Przez punkt P(a,b,c), gdzie a,b,c>0 poprowadzić płaszczyznę tak, aby objętość czworościanu jaki ona odcina na osiach układu współrzędnych była najmniejsza. równanie płaszczyzny

	x		y		z
π:		+		+		=1
	A		B		C

	a		b		c
π:		+		+		=1
	A		B		C

	1
v(A,B,C)=		ABC
	6

dv		1
	=		BC=0
dA		6

dv		1
	=		AC=0
dB		6

dv		1
	=		AB=0
dC		6

ale stąd mam punkt stacjonarny K=(0,0,0), ale to jest niemożliwe jakieś wsparcie ?

Stary Rok: Wsparcia dzisiaj szukaj na Sylwestrowym Balu

Rok2015: Zatwierdzone

Saizou : bardzo śmieszne, ale ja tu pytam się na poważnie xd

Helena: czemu liczysz pochodne cząstkowe po A, B czy C? przecież współrzędne tych punktów zależą od (a,b,c)

Saizou : nie ogarniam, dlaczego ?

Godzio: Ja bym to tak robił: Weźmy dwa punkty na osi OX i OY: Q(A,0,0) i W(0,B,0) Masz dany punkt P(a,b,c), on Ci wyznaczy punkt na osi OZ. Wyznacz wektor QP i QW, następnie poprowadź płaszczyznę wyznaczoną przez te wektory, i znajdź punkt przecięcia z OZ.