problem z przedziałami olla: Rozwiąż algebraicznie i graficznie nierówność: |x²+6x+11|<x+7 wyliczam deltę, ale nie da się i jak mam ustalić przedziały ? Będą wszystkie liczby

Jerzy: 1) założenie: x + 7 > 0 2) ⇔ − x − 7 < x² + 6x + 11 < x + 7

ICSP: x² + 6x + 11 > 0 dla dowolnego rzeczywistego x, więć wprost z definicji wartośći bezwzględnej : |x² + 6x + 11| = x² + 6x + 11 Twoja nierówność można zapisać równoważnie: x² + 6x + 11 < x + 7 x² + 5x + 4 < 0 (x +4)(x+1) < 0 x ∊ (−4 ; − 1)

Jerzy: nie zauważyłem,że trójmian jest stale dodatni

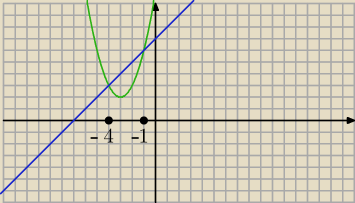
Jerzy: i graficznie

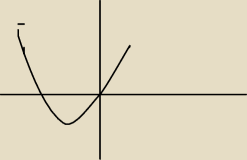
olla: Teraz to się wydaje łatwe, robię drugi przykład: |x²+4x+3|≥−x+3 z pierwszego przedziały 0 i −5 1.Założenie (−∞,−5) i <0,∞) dodatnie czyli x²+4x+3≥−x+3 stąd x²+4x+3+x+3=0 Δ=1 x=−3 i x=−2 czyli żadna nie należy do przedziału 2.założenie <−5,0) ujemne i tu jest problem: −x²−4x−3+x+3=0 −x²−3x−6=0 Δ<0 ja to chyba w ogóle źle pojmuję −proszę o pomoc

olla: czy te założenia są dobre?

ICSP: skąd liczby −5 oraz 0 ?

olla: z x2+4x+3 poszukałam kiedy są wartości nieujemne kiedy ujemne delta i miejsce zerowe poprawiam Δ=16−12=4 Δ=2 x=−3 x=−1 i takie będą przedziały dodatnie /trochę skrótowo piszę/ 1.Założenie (−∞,−3) i <−1,∞) co i tak stawiam mnie przed ścianą jeśli idzie o drugie założenie

ICSP: 1. x ∊ (− ∞ ; − 3] ∪ [−1 ; + ∞) x² + 4x + 3 ≥ −x + 3 ... 2. x ∊ (−3 ; −1) −(x² + 4x + 3) ≥ −x + 3 ...

olla: właśnie przed chwilą wpadłam na ten pomysł dzięki, dalej pójdzie

Helena: no źle po 1^o rozwiązujesz nierówność, a nie równanie, kolejno co do 1) Założenie gdy x jest elementem (−∞,−3>∪<−1,∞) x²+4x+3+x−3≥0 x²+5x≥0 x(x+5)≥0 stąd i z założenia x∊(−∞,−5>∪<0,∞) do 2) Jeżeli x∊(−3,−1) dostajemy −x²−4x−3+x−3≥0 wtedy −x²−3x−6≥0 Δ<0 brak rozwiązań ponieważ cała parabola znajduje się pod osią X Rozwiązanie to x∊(−∞,−5>∪<0,∞)

olla: podałaś zły wynik w książce jest inaczej pomieszaliście mi w głowie

olla: Jest tak jak podał ICSP: i mi tez tak wyszło

ICSP: x ∊ (− ∞ ; − 5] ∪ [0 ; + ∞)

olla: nie ! x ∊ (− ∞ ; − 5] ∪ [1 ; + ∞)

ICSP: http://www.wolframalpha.com/input/?i=%7Cx%5E2%2B4x%2B3%7C%E2%89%A5%E2%88%92x%2B3

olla: to dlaczego mnie zapytałeś skąd te liczby: ICSP: skąd liczby −5 oraz 0 ? Byłam na dobrej drodze nie napisałam sumy co słusznie helena zauważyła bo nie umiem jej znaleźć. robiłam zawsze tego typu zadania tak jak helena napisała potem zadałeś to pytanie o liczby,które zasiało mi w głowie mętlik więc zmieniłam co potwierdziłeś wpisem ICSP: 1. x ∊ (− ∞ ; − 3] ∪ [−1 ; + ∞) teraz to się zastanawiam czy jeszcze coś w ogóle rozumiem, ale jak widać nie do końca zawsze tu dobrze piszecie mimo wszystko DZIĘKI OGROMNE ZA CZAS I CIERPLIWOŚĆ

Helena: Podałam Ci pełne rozwiązanie zadania, żebyś następnym razem nie pisała głupot

olla: Ok, na początku podobnie kombinowałam, ale potem zaufałam mądrzejszym i poszło źle, a w książce wynik musi być więc błędny.

olla: ICSP: ogromne dzięki, dzięki za link można super poćwiczyć zamiast wam głowę suszyć, wszystkiego dobrego w nowym roku BARDZO DZIĘKUJĘ !

Helena: olla, zaufanie to trochę za mało, trzeba jeszcze umieć skorzystać z rady, która oczywiście jest jak najbardziej dobra, sporo już się nauczyłaś, teraz uporządkuj troszkę tę wiedzę i będzie dobrze, a Nowym 2016 Roku życzę jak najwięcej poprawnych wyników