planimetria czworokaty ania111: Punkty M i N dzielą ramiona trapezu w stosunku 2:1 (licząc od dłuższej podstawy). Wyraź długość odcinkaMN za pomocą długości podstaw trapezu a i b (a >b).

Kacper:

1		2
	a+		b
3		3

Eta: Potwierdzam

	a+2b
i zapis bardziej "elegancki"
	3

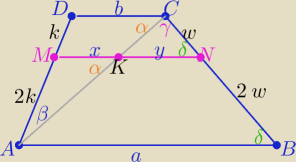
Eta: |MN|=x+y Z podobieństwa trójkątów AKM ∼ACD z cechy (kkk) i ABC ∼ KNC z cechy (kkk)

b		3k		a		3w
	=				=
x		2k		y		w

	2		1
to x=		b y=		a
	3		3

|MN|= x+y=.......

PW: Ja tak dla porządku zapytam (jak ten pilny mały Jaś co w każdej klasie się znajdzie): − A skąd wiadomo, że te kąty są odpowiednio równe?

Eta: MN∥ AB ∥CD ( perfekcjonisto Z lenistwa nie lubię pisać "elaboratów" ( bo nie lubię przedmiotów humanistycznych ) Właśnie z tej przyczyny wybrałam "matmę"

Eta: A czy "mały Jaś" słyszał o Talesie? czy tylko o Pitagorasie?

PW: A teraz zupełnie poważnie pytam: − Czy maturzysta przyjmujący milcząco, że MN jest równoległy do podstaw, otrzyma pełną punktację za rozwiązanie? I z ciekawości zapytam (ale maturzystów, nie Ciebie ) − jak brzmi uzasadnienie?

Metis: Gdyby dany odcinek nie był równoległy nie zachodzilaby własnośc taka że punkty M i N dziela ramiona w stosunku 2 do 1 . Mogę się mylić , i pisać głupoty. Nie lubię planimetrii i nie zbyt ja rozumiem.

Kacper: PW ja by maksa nie dał, ale na maturze myślę, że wystarczy napisać, że są równoległe i uznają Czego oni na maturze nie uznają

Metis: Jeżeli potrafimy udowodnić, że punkty M i N są środkami ramion, to tym samym wykażemy, że odcinek MN, łączący środki tych ramion jest równoległy do podstaw. Punkty M i N są środkami ramion, zapewnia Nam to własność tego trapezu o podziale ramion w stosunku 2 do 1 , zatem odcinek MN jest równoległy do podstaw tego trapezu.

PW: Ależ nie są środkami ramion − patrz dobry rysunek Ety.

paulinka: to z czego to wynika w końcu ? ze ta prosta jest rownoległa

paulinka: w czym którym z trojkatow ten tales zachodzi

5-latek :