nierówność z wartością bezwzględną
olla: Równania poszły ładnie, a tu ostatnia nierówność i klops
rozwiąż nierówność:
x
2+4x+|x−3|+5>0
przedziały to: (−
∞3) oraz<3,
∞)
1.(−
∞3)
x
2+3x+8 Δ<o brak rozwiązania
2.
x
2+5x+2
Δ
√17
x=(−5−
√17):2≈ −4,5
x=(−5+
√17):2≈ −0,4 i dalej już n ie robię bo to są głupoty, gdyż rozwiązaniem jest x∊R
glapię się i glapię i nie mogę znaleźć błędu

30 gru 18:31
olla: proszę choć o jakąś wskazówkę, bo robię któryś raz i wciąż wychodzi to samo...:(
30 gru 18:49
Kacper:
Napisz do mnie na gadu, to lepiej pomogę. (8959267)
Delta ujemna nie wskazuje brak rozwiązań w nierównościach kwadratowych

30 gru 18:52
olla: nie mam gg
Delta ujemna nie wskazuje brak rozwiązań w nierównościach kwadratowych czyli

30 gru 18:55
olla: Kacper ulituj się ...
30 gru 18:55
Kacper:
Dobrze to na początek takie zadanie:
Podaj te argumenty, dla których funkcja f(x)=x2+4x+3 przyjmuje wartości dodatnie.
Umiesz tutaj rysować?
30 gru 18:57
teo:
x
2+4x+|x−3|+5>0
1)x∊(−
∞,3)
|x−3|=−(x−3)
x
2+4x−(x−3)+5>0
x
2+4x−x+3+5>0
x
2+3x+8>0
Δ=9−32<0⇔trójmian
y=x2+3x+8 przyjmuje wartości dodatnie dla każdego x<3
(parabola skierowana do góry i brak miejsc zerowych)
x∊(−
∞,3)
lub
2) x≥3
|x−3|=x−3
x
2+4x+x−3+5>0
x
2+5x+2>0
Δ=25−8=17
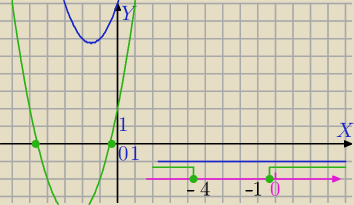
| | −5−√17 | | −5+√17 | |
x1= |
| ≈−4,6 lub x2= |
| ≈−0.4 |
| | 2 | | 2 | |
| | −5−√17 | | −5+√17 | |
x< |
| lub x> |
| |
| | 2 | | 2 | |
=============================
Suma rozwiązań: x∊R
30 gru 19:02
olla:
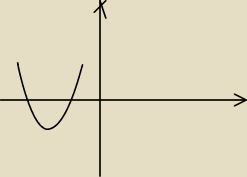
Nieudolnie, ale spróbuję ramiona w górę x= −3 i x= −1 (nie umiem nanieść cyfr na wykres)
wartości dodatnie (−
∞, −3) (−1,
∞)
30 gru 19:04
Kacper:
Dobrze a teraz dla jakich argumentów funkcja f(x)=x
2+x+1 przyjmuje wartości dodatnie?

Widzę, że dostałaś gotowca

30 gru 19:08
olla: teo dziękuję czyli drugie założenie miałam ok, ale nie wiedziałam, że w pierwszym będzie
rozwiązaniem x∊(−∞,3) zupełnie nie wyobraziłam sobie tego, tylko mechanicznie pomyślałam skoro
brak miejsc zerowych to brak rozwiązania−DZIĘKI OGROMNE Kacper i teo dobrej nocy życzę
30 gru 19:11
teo:

19:02 niebieska linia ( w dolnym) powinna "lecieć" od 3 w lewo, ale odpowiedź dobra.
Suma przedziałów: (−
∞,
∞)
odp.
x∊R
30 gru 19:33



 x2+4x+|x−3|+5>0
1)x∊(−∞,3)
|x−3|=−(x−3)
x2+4x−(x−3)+5>0
x2+4x−x+3+5>0
x2+3x+8>0
Δ=9−32<0⇔trójmian y=x2+3x+8 przyjmuje wartości dodatnie dla każdego x<3
(parabola skierowana do góry i brak miejsc zerowych)
x∊(−∞,3)
lub
2) x≥3
|x−3|=x−3
x2+4x+x−3+5>0
x2+5x+2>0
Δ=25−8=17
x2+4x+|x−3|+5>0
1)x∊(−∞,3)
|x−3|=−(x−3)
x2+4x−(x−3)+5>0
x2+4x−x+3+5>0
x2+3x+8>0
Δ=9−32<0⇔trójmian y=x2+3x+8 przyjmuje wartości dodatnie dla każdego x<3
(parabola skierowana do góry i brak miejsc zerowych)
x∊(−∞,3)
lub
2) x≥3
|x−3|=x−3
x2+4x+x−3+5>0
x2+5x+2>0
Δ=25−8=17
 Nieudolnie, ale spróbuję ramiona w górę x= −3 i x= −1 (nie umiem nanieść cyfr na wykres)
wartości dodatnie (−∞, −3) (−1,∞)
Nieudolnie, ale spróbuję ramiona w górę x= −3 i x= −1 (nie umiem nanieść cyfr na wykres)
wartości dodatnie (−∞, −3) (−1,∞)
 Widzę, że dostałaś gotowca
Widzę, że dostałaś gotowca
 19:02 niebieska linia ( w dolnym) powinna "lecieć" od 3 w lewo, ale odpowiedź dobra.
Suma przedziałów: (−∞,∞)
odp.
x∊R
19:02 niebieska linia ( w dolnym) powinna "lecieć" od 3 w lewo, ale odpowiedź dobra.
Suma przedziałów: (−∞,∞)
odp.
x∊R