wielomiany plot21: dla jakich wartości parametru m równanie (x+2)[(m+1)x²−4mx+m+1]=0 ma trzy różne pierwiastki ujemne? zrobiłem warunki dla g(x)=(m+1)x²−4mx+m+1 1. delta>0 2. m+1 różne od zera 3. x₁+x₂<0 4. x₁+x₂>0 5. g(−2) różne od zera ale nie wychodzi mi , odp. powinna być (−&,−1) suma (1,+&) Prosze o pomoc

Kacper: Warunki prawie ok (w jednym miejscu x₁*x₂), zapewne błędy rachunkowe.

plot21: x1*x2>0 ?

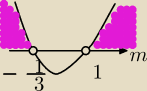
Jack: 1. Δ>0 Δ_x = 16m² − 4(m+1)² = 16m² − 4(m²+2m+1) = 12m² − 8m − 4 12m² − 8m − 4 >0 Δ_m = 64 + 16 * (12) = 256 √Δ_m = 16

	8 − 16		1
m1 =		= −
	24		3

m₂ = 1

	1
m ∊ (−∞; −		) U (1;∞)
	3

2. m ≠ −1 3.

	b
−		<0
	a

4m
	<0
m+1

m ∊ (−1;0) 4. x₁ * x₂ > 0

c
	> 0
a

m+1
	> 0
m+1

1>0 m ∊ R 5. g(−2) = 13m + 5 13m + 5 ≠ 0

	−5
m ≠
	13

Podsumowanie : m ∊ ∅ DDD

Jack: 3 warunek wyklucza cala dziedzine odrazu...cos jest nie tak ; d

Kacper: To czytaj ponownie, ponownie i szukaj błędu (jest)

Jack: ale w 3cim musialem zrobic blad...

Jack: Nwm gdzie jest blad... sie nie zgadza cos

Kacper: Sprawdzaj ponownie

Jack: 4m(m+1) zwsz bedzie dodatnie

Kacper: Nie szukaj błędu w obliczeniach, tylko w wyznaczaniu części wspólnej zbiorów

Jack: zbior (−1;0) z czym kolwiek da nam (−1;0) jesli chodzi o czesc wspolna...

Kacper: To czemu piszesz m∊∅? To, że inna jest odpowiedź, to potem się zajmiemy.

Jack: no ale nie jest taka jak w ksiazce, czyli wszystko mam zle, to po co mam cokolwiek sprawdzac...

Kacper: A skąd wiesz, że książka się nie myli? że autor dobrze treść przepisał?