Obliczyć granicę funkcji
Karola: obliczyć granicę funkcji f(x) = √(x−1)/(1+x)
przy x → 1+
x→ 1−
x→+∞
x→−∞
30 gru 12:31
Kacper:
Własne pomysły?
30 gru 12:32
Arturek_lat_7: Jej pomysł to napisanie tutaj
30 gru 12:36
Kacper:
Właśnie zauważyłem
30 gru 12:44
Karola: ; (
30 gru 12:49
Kacper:
Myślisz, ze damy ci gotowca?
30 gru 12:50
Karola: można wytłumaczyć
30 gru 12:58
Karola: choć w sumie, nie kłopocz sie, poszukam dalej w necie, pewnie znajdę w końcu
30 gru 12:59
Arturek_lat_7:
szukaj szukaj studentka ... w lutym będą poprawki, do tego czasu może znajdziesz
30 gru 13:00
Jack: usun niewymiernosc? ; d
30 gru 13:01
azeta: podejrzewam, że przykład jest źle przepisany. albo granica jest w (−1) albo licznik nam się
zamienił z mianownikiem
30 gru 13:01
Karola: dobrze jest przepisana
30 gru 13:02
30 gru 13:04
azeta: | | x−1 | | 1−1 | |
jeśli byłby dobrze przepisany to limx→1+ √ |
| =limx→1 √ |
| =0, zapewne |
| | x+1 | | 1+1 | |
chodzi o granice w (−1), a nie 1
30 gru 13:04
Jack: jak rozumiem twoja funkcja wyglada tak :
z jedynka chyba wiesz co bedzie? jak podstawisz jeden ...wyjdzie 0 przez liczbe czyli 0...
30 gru 13:05
Jack: lim x−>
∞ i do −
∞ wyjdzie taki sam
czyli
| | x−1 | | x+1−2 | |
lim √ |
| = lim √ |
| = lim √1 − 2x+1 = √1 = 1 |
| | x+1 | | x+1 | |
pozdrawia licealista
30 gru 13:10
Karola: ja też chodzę do liceum, nie wiem o co wam chodzi, ehhh dzięuję za pomoc
30 gru 13:13
Jack: aa to fajno
tam na pewno lim x−>1? czy moze jednak − 1?
30 gru 13:13
Karola: −1
30 gru 13:15
Jack: no to sie nam nieco zmieni
lim x−>−1
− :
| | x−1 | | −2 | |
lim √ |
| = lim √ |
| = +∞ |
| | x+1 | | 0− | |
lim x−> −1
+ :
| | x−1 | | −2 | |
lim √ |
| = lim √ |
| = nie istnieje...bo nie ma pierwiastkow z liczb ujemnych |
| | x+1 | | 0+ | |
(chyba ze mowa o studiach, ale pisalas ze jestes z liceum wiec zakladam ze nie
)
30 gru 13:24
Karola: a to nie będzie w tym drugim po prostu −∞?
30 gru 13:26
Kacper:
Zaczynamy od dziedziny, bo badanie granicy jeśli funkcja nie jest określona w pewnym
sąsiedztwie funkcji nie ma sensu.
30 gru 13:28
Jack: @Karola
a ile wynosi √−1 ?
30 gru 13:54
Karola: no a −1 / 0+ to nie działa na takiej zasadzie jak −1 / 0− = +
∞ 
30 gru 14:04
Karola: wtedy będzie pierwiastek z −∞ a to wciąż −∞, tak ?
30 gru 14:05
Karola: tylko sie nie śmiej w ogóle tego nie ogarniam wszystkiego ^^
30 gru 14:05
Jack: | | −1 | | −1 | | 1 | |
To raczej cos w tym stylu |
| = |
| * |
| => + |
| | 0− | | −1 | | 0 | |
a tamto
oczywiscie taki zapis jest raczej nie poprawny. Jest on tylko do pokazania o co kaman hir tutaj
30 gru 14:07
Karola: ok czaję
30 gru 14:38
Kacper:
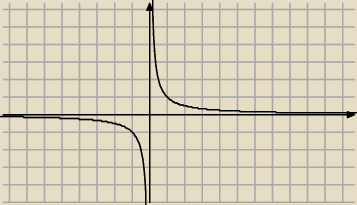
Proponuje zawsze w takim przypadku przypomnieć sobie wykres hiperboli
30 gru 14:42