wykaz, ze few:

	|AC|*|CB|
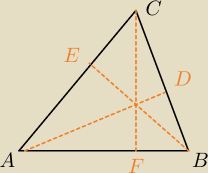
Wykaż, że jeżeli |AD|+|BE|=|CF| to |AB|=
	|AC|+|CB|

Kolorem pomarańczowym są zaznaczone wysokości trójkąta.

Kacper: Czyżby jakiś konkurs?

few: nie, z arkuszy maturalnych

Jack: Proponuje uzyc 3 wzory na pole trojkata..kazdy z inna wysokoscia

Jack: Ulozyc*

Kacper: Z jakich jeśli można wiedzieć?

Kacper: Jack możesz się wykazać

Jack: Hehehe

===: oczywista oczywistość

1		1
	+		=1
2		2

Eta: |AB|=c , |AC|=b, |BC|=a , |AD|=h_A, |BF|=h_b , |CD|=h_C

	b		b
ha=		*hb , hc=		*hb
	a		c

b		b		ab
	*hb+hb=		*hb /:hb ⇒c=
a		c		a+b

	|AC|*|CB|
|AB|=
	|AC|+|CB|

c.n.w

===: albo wprost

|AB|*|AC|+|AB|*|BC|
	=1
|AC|*|BC|

|AB|		|AB|
	+		=1
|BC|		|AC|

1		1
	+		=1
2		2

few:

	1		1
Skąd na końcu		+		?
	2		2

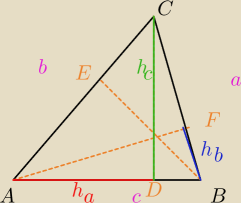
Jack: @Eta Jak Ty z tego takie równania ułożyłaś te odcinki sa bez sensu : o

Kacper: Zapewne pomyłka, bo |AF|=h_A, |BE|=h_B, |CD|=h_C

===: skoro |AD|+|BE|=|CF| ... to masz trójkąt równoramienny w którym 2|AB|=|BC|=|AC|

few: Trójkąt ABC jest równoramienny? Przecież tak być chyba nie musi

===: ... MUSI ! Przeczytaj post Jacka z 10:41

Jack: @Kacper mam taka nadzieje, bo inaczej, to ja wgl sie nie znam na ukladaniu rownan w trojkacie ; d

===: to Ty Jack nakaszaniłeś w swoim rysunku z 12:59 ... a potem "masz migawy" do mojej Kumpeli Ety (nakręciłeś w oznaczeniu punktów ... porównaj z rysunkiem wyjściowym)

few: To dlaczego ja narysowałem trójkąt, który spełnia warunki zadania i nie jest równoramienny?

Jack: @=== o kurcze, faktycznie cos nachrzanilem...ale jak rysowalem na kartce to tez mi nie wyszlo...czytac chyba nie umiem]

===: ... z przeproszeniem pierdoły narysowałeś ... sprawdź czy na Twoim rysunku zachodzi |AD|+|BE|=|CF|

===: to do few

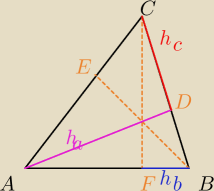
Jack: Ale zreszta i tak wyjdzie badziewie xD w sensie chyba Eta miala co innego na mysli ^^

===: Jack ... chyba Cię zaćmiło Ona tzn Ecinka zapisała dokładnie ro co Ty napisałeś w poście z 10:41 (chyba że to nie Ty ?) h_a*a=h_b*b

few: Panie ===: proszę (dobrze, że moja nauczycielka nauczyła nas geogebry http://zapodaj.net/a9c867d657318.jpg.html Proszę o komentarz i ewentualnie wyjaśnienie moich wątpliwości

few: Coś się nie zgadza? Nigdzie nie ma informacji, że to ma być trójkąt ostrokątny. Nie potrafisz logicznie mi wytłumaczyć tego, że niby ten trójkąt ma być równoramienny, a mój rysunek dowodzi, że być nie musi.

few: Mój błąd, bo taki rysunek zrobiłem na początku.

few: Na dodatek agresywny jesteś, obraziłem cię gdzieś?

Jack: === [Jack] , Jack i Jack to ja. Radze przeczytac dokladnie jak paniEta oznaczyla owe boki i wysokosci oraz porownac na rysunku

few: Jack nie radzę go słuchać, bo napisał rozwiązanie i jak chciałem dopytać dlaczego, to zaczął mnie obrażać. ps. Pani Eta serdecznie dziękuję Proszę kogoś o obiektywne wypowiedzenie się w tej sprawie

few: Widzę, że nie można normalnie pomocy dostać...

utem:

	a		b
Jeżeli c=		albo c=		, to wtedy Δ przy podanych założeniach w zadaniu, jest
	2		2

równoramienny, bo

a		a*b
	=
2		a+b

a*(a+b)=2ab, a>0 i b>0 a²+ab=2ab a²−ab=0

	a
a(a−b)=0⇔a=b ⇔ΔABC jest równoramienny o bokach: a,a,		.
	2

=======================================

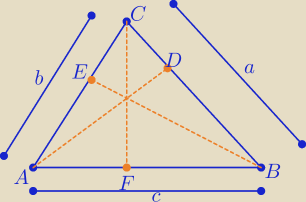
Eta: Każdy "myślący" powinien zauważyć pomyłkę w oznaczeniach Poprawiam |AB|=c, |AC|=b, |BC|=b |AD|=h_a, |BE|= h_b , |CF|=h_c

	a*ha		b*hb		c*hc
Z równości pól :		=		=		⇒
	2		2		2

	b		b
że ha=		*hb i hc=		*hb
	a		c

z warunku zadania :

	b		b
ha+hb=hc ⇒		*hb+hb=		*hb /: hb
	a		c

	a+b		b		ab
		=		⇒ c=
	a		c		a+b

	|AC|*|CB|
wracając do oznaczeń: |AB|=
	|AC|+|CB|

c.n.w

Eta: W tym zadaniu : nie pytają jaki to trójkąt?

few: Dziękuję za rozwianie wątpliwości Czyli ten trójkąt nie musi być wcale równoramienny?

Eta: Ten trójkąt dodatkowo jest równoramienny ( co wyjaśniła Mila Dowód dotyczył podanej równości ... więc nie musimy uzasadniać ,że jest to trójkąt równoramienny

few:

	a		u
Ale Mila napisała: Jeżeli c=		lub c=		, to jest równoramienny, a tego chyba nie
	2		2

było w treści zadania

Eta:

	ab
Jeżeli c=		⇒ że trójkąt ABC jest równoramienny
	a+b

	a
bo dla c=		i b=a i a
	2

mamy:

	ab		a*a		a2		a
c=		⇒ c=		=		=
	a+b		a+a		2a		2

few: A zerknij jak możesz na mój rysunek. Owszem on może być równowamienny, ale czy zawsze musi? wg mnienie

Jack: Czyli byla pomylka w oznaczeniach ! wiedzialem

Eta: To,że ten trójkąt jest równoramienny wynika z warunku zadania: że h_a+h_b= h_c

Eta: Hej "niepokorny Jacusiu"

Jack: niepokorny i łagodny jak baranek...

few: Nie rozumiem w jaki sposób to wynika z tego warunku

Jack: duzo latwiej sie liczy ekstrema funkcji dwoch zmiennych niz jakies zadania z planimetrii...

Jack: few...napisal to utem 18;03

Jack: ale raczej wolalbym "pokorny" jacuś xd

Eta: Na maturze będą co najmniej trzy zadania z planimetrii I co wtedy? :...........

5-latek: Jack napisala to utem Pozdrawiam Przeciez masz na imie Michał . To dlaczego jacuś ?

Jack: na pewno latwiejsze niz te co licze xd

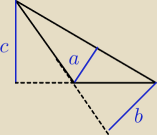
few: W tym trójkącie a+b=c a nie jest równoramienny już nie wiem poddaje się nigdy tego nie zrozumiem

Jack: jak juz ma byc jacus to niech bedzie jacus... aczkolwiek najbardziej pasuje mi Jack...

Jack: Jack (dżak)

utem: Czytaj uważnie , co napisano, jeżeli spełnione są założenia podane w zadaniu

	ab		a
( z tego wynika, że c=		) i dodatkowo zakładam, że c=		,
	a+b		2

to trójkąt jest równoramienny.

	a		b
Teraz pytanie, czy z warunków zadania wynika, że c=		albo c=		.
	2		2

W zadaniu nie pytają , jaki to trójkąt. Bez założenia, że Δ jest równoramienny , nasz ładny jasny dowód, Ety. Koniec. Kropka. Pomyślę , nad satysfakującym Cię, wykazaniem lub zaprzeczeniem, że zawsze jest to Δ równoramienny.

utem: zakł. , że h_a≠h_b h_a=k*h_b Z zał. h_a+h_b=h_c k*h_b+h_b=h_c h_b*(k+1)=h_c

c*hc
	*(k+1)=hc
b

	a*b		b
c*(k+1)=b⇔		=		⇔
	a+b		(k+1)

a		1
	=		⇔
a+b		k+1

a*(k+1)=a+b a*k+a=a+b a*k=b

	a*a		a
dla k=1 masz Δ równoramienny (i c=		=		), dla k>0 i k≠1 Δ nie jest
	a+a		2

równoramienny. Kacper, Eta.., zobaczcie, czy jest jeszcze coś, z czym trzeba się liczyć.

Eta: dla Mili

few: Czyli cały czas miałem rację, że on nie musi być równoramienny

Eta: Ten przy takim warunku, który masz w zadaniu: jest równoramienny

utem: Dziękuję Proszę, nie ujawniaj mnie, bo widziałaś co hejterzy wczoraj robili.

utem: few te róże to Twój zachwyt dla Ciebie? Czy podziękowanie dla nas?

few: miało być dla ciebie w ramach podziękowania, ale Eta cały czas twierdzi, że jest on równoramienny.

Tadeusz: Piszesz few ... "dobrze, że moja nauczycielka nauczyła nas geogebry" ... szkoda tylko, że nie nauczyła Cie MYŚLEĆ Nic to, że Jack, Mila, Eta i inni piszą, że trójkąt z treści zadania RÓWNORAMIENNYM BYĆ MUSI ... ty i tak swoje ... ni chwili zastanowienia ... namysłu ... od 13:30 do 22:41 "swoje" Nawet nie czytasz tego co inni wytłumaczyć ci usiłują Kiedyś nadawałbyś się do pewnej "organizacji" ... tam oceniali przydatność na zasadzie "głupi bo głupi ale uparty".

Tadeusz: Pani jeszcze w podstawówce tłumaczyła Ci wzór na pole trójkąta "jedna druga podstawy razy wysokość na nią opuszczona" Powinieneś wiedzieć, że na dowolny bok wysokość opuścić możesz ... zatem w danym trójkącie iloczyn długości podstawy i wysokości na nią opuszczonej jest const. A skoro dwie wysokości mają tą samą długość ... to i podstawy na które są opuszczone równe być muszą. A skoro dwa boki trójkąta są równe Skoro pytasz tu o coś ... to przeczytaj choć uważnie to co ci piszą

5-latek: Czesc Tadeusz . Wszystkiego dobrego w Nowym roku I dalej sa takie " organizacje'' na zasadzie mierny ,bierny ale wierny

few: Panie Tadeuszu. Bardzo cenie waszą pomoc ale Pani Mila nigdzie nie napisała ze ten trójkat musi być równoramienny. prosze przeczytać post 21:49 i kolejny 22:16 Mila tłumaczy tam ze taki trójkat nie musi byc równoramienny Prawdą jest, ze o równoramienny o bokach c, 2c, 2c spełnia warunki zadania.

Tadeusz: MYŚLENIE CZASEM BOLI ...

Tadeusz: post z 22:16 (w sumie już nie wiem czyj Mila to czy utem) to zawiły dowód na to, że masło jest z mleka. Poczytaj dokładnie na początku założenie, że h_a≠h_b czyli "wspak" do treści zadania. założenie, że h_a=kh_b ... a na końcu dla k=1 .... czyli dla h_a=h_b ... równoramienny.

few: Dobrze, to proszę o rozwiązanie takiego zadania. Mamy trójkat o bokach a, b, c Wykaż, że jeżeli h_a+h_b=h_c, to trójkąt jest równoramienny. Wy to usilnie twierdzicie, a ja uważam, że to nie zawsze jest prawdą.

Tadeusz: Nie da się z tobą dyskutować ... bądź łaskaw przeczytać co napisałem o 11:19 i włącz myślenie

few: Tadeusz, ja bardzo dobrze rozumiem to co piszesz o 11:19, ale gdzie w zadaniu jest mowa, że te wysokości są równe? jak z warunku h_a+h_b=h_c może wynikać, że h_a=h_b? Przecież te wysokości mogą być równe 2,3,5.

Tadeusz: a to co napisałeś to zupełnie inne założenia !

few: Jaki inne założenia? Zadanie 30.12 10:18 Wykaż, że jeśli |AD|+BE|=|CF| − to są zalozenia, czyli h_a+h_b=h_c. Jak można na tej tylko podstawie twierdzić ze trójkąt ABC jest równoramienny?

misiak: można czy nie można?