Walec Łysy: Odcinek łączący środek dolnej krawędzi podstawy walca z punktem na brzegu górnej podstawy tworzy z tymi podstawami kąt α. Wyznacz objętość walca, jeśli przekątna jego przekroju osiowego ma długość d. Do tej pory zrobiłem tyle: Narysowałem przekrój osiowy walca z którego wyszło mi, że h/r=tgα ⇒ h=r tgα ⇒ r=tgα/h A z twierdzenia Pitagorasa h²+(2x)²=d² ⇒ r²=(d²−h²)/4 Podstawiłem to pod wzór na objętość walca V=πr²h Najpierw podstawiłem h V=π r³ tgα Teraz r² V=π [(d²−h²)/4]⁽3/2) tgα I tutaj utknąłem w martwym punkcie. Będę wdzięczny za wskazówki, znalezione błędy w moim toku rozumowania i rozwiązanie zadania. Prawidłowa odpowiedź do zadania to V=π d³ (1/(4+tg²α))⁽3/2) tgα Ps. Pod koniec mojego opisu te całe nawiasy są podnoszone do potęgi 3/2, ale nie umiem tego poprawnie zapisać

dero2005:

h
	=tgα
r

h= rtgα (2r)²+h²=d²

	d
r =
	(4+tg2α)12

	d
h=		*tgα
	(4+tg2α)12

	1
V= πr2h = πd3		*tgα
	(4+tg2α)32

Łysy: Nie mogę dojść skąd wyszło r = d/[(4+tg2α)^3/2]

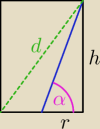
dero2005: dane: d,α

h
	= tgα
r

h = rtgα (2r)² + h² = d² 4r² + r²tg²α = d² r² (4 + tg²α) = d²

	d2
r2 =
	4 + tg2α

	d
r =
	(4 + tg2α)12

	d
h =		*tgα
	(4 + tg2α)12

	d2		d
V = πr2h = π		*		*tgα =
	(4+tg2α)22		(4+tg2α)12

	1
= πd3*		*tgα
	(4+tg2α)32