 Mógłby ktoś wytłumaczyć?
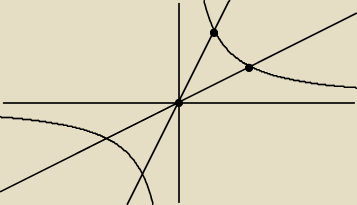
Narysuj i wyznacz pola poniższych zbiorów
Mógłby ktoś wytłumaczyć?
Narysuj i wyznacz pola poniższych zbiorów
| 1 | 1 | |||
a) A = {(x,y)∊R2: 0 ≤ y ≤ | , y ≤ 2x, y ≥ | x | ||
| x | 2 |
| 1 | ||
PUNKT P1 (przecięcie y=2x i y= | ||
| x |
| 1 | √2 | √2 | ||||
2x= | ⇒ x = | } lub x= − | ||||
| x | 2 | 2 |
| 1 | 1 | ||
x = | ⇒ x=√2 lub x=−√2 | ||
| 2 | x |
| √2 | 1 | 3 | ||||
∫ indeks górny | indeks dolny 0 z (2x− | x)dx = | j2 | |||
| 2 | 2 | 8 |
| √2 | ||
nie bardzo wiem dlaczego zostały tutaj wybrane przy oznaczeniu całki | } i 0 | |
| 2 |
| 1 | ||
oraz skąd proste y=2x i y= | x | |
| 2 |
| √2 | 1 | 1 | 3 | |||||
S2 to całka o indeksie górnym √2 i dolnym | z ( | − | x)dx = ln2 − | |||||
| 2 | x | 2 | 8 |
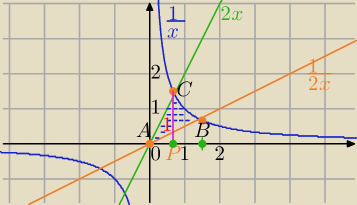 Musisz trójkąt , tak podzielić , abyś miała obszary normalne względem osi OX, ( albo OY)
C:
Musisz trójkąt , tak podzielić , abyś miała obszary normalne względem osi OX, ( albo OY)
C:
| 1 | ||
2x= | , x>0 | |
| x |
| √2 | ||
x= | ||
| 2 |
| √2 | ||
y=2* | =√2 | |
| 2 |
| √2 | ||
C=( | ,√2) | |
| 2 |
| √2 | ||
P=( | ,0) | |
| 2 |
| 1 | 1 | ||
x= | , x>0 | ||
| 2 | x |
| 1 | |
x2=1 | |
| 2 |
| √2 | ||
y= | ||
| 2 |
| √2 | ||
B=(√2, | ) | |
| 2 |
| √2 | ||
P1−Całka (górna funkcja − dolna funkcja, tak zmienia się y), granice od x=0 do x= | ||
| 2 |
| 1 | 3 | 3 | ||||
P1=x=0∫x=√2/2(2x− | x) dx =∫0∫√2/2( | x) dx=[ | x2]0√2/2= | |||
| 2 | 2 | 4 |
| 3 | √2 | 3 | 1 | 3 | ||||||
= | ( | )2−0= | * | = | ||||||
| 4 | 2 | 4 | 2 | 8 |
| √2 | ||
P2 − całka górna funkcja − dolna funkcja , granice x= | do x=√2 | |
| 2 |
| 1 | 1 | 1 | ||||
P2=x=√2/2∫x=√2( | − | x) dx=[lnx− | x2]x=√2/2x=√2= | |||
| x | 2 | 4 |
| 1 | √2 | 1 | 1 | |||||
=ln√2− | *2−ln( | )+ | * | = | ||||
| 4 | 2 | 4 | 2 |
| 1 | 1 | 3 | ||||
=ln√2− | −ln√2+ln(2)+ | =ln(2)− | ||||
| 2 | 8 | 8 |

