stereometria 5-latek: Zadanie dla Metisa . Tresc: ======== Prawidlowy ostroslup czworokątny ma bok podstawy rowny a i sciany boczne nachylone pod kątem α do plaszcyzny podstawy . Przez jedna z krawędzi podstawy poprowadzono plaszczyzne nachylona pod kątem β do podstawy (β<α) . Oblicz pole powstałego przekroju uwazajac a ,α,β za wiadome .

Metis: Spróbuję

5-latek: I jeszcze jedno Tresc ======= Udowodnij ze iloczyn promieni czterech kol : kola woisanego i i trzech kol dopisanych , rowna się kwadratowi pola trojkata r*r₁*r₂*r₃= S²

Jack: Banał

Metis: Mam już rysunek. Z wiadomości: " Prawidlowy ostroslup czworokątny" wydawałoby się, że nie będzie problemu, ale dużo liczenia.

5-latek: Tak zgadza się − trochę będzie liczenia

Metis: http://i.imgur.com/kDEMUeA.jpg Rysunek, ale niestety nie wiem gdzie zaznaczyć kąt β i od czego w ogóle zacząć .

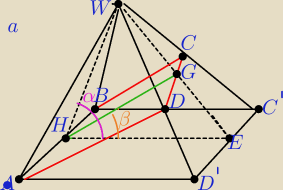
5-latek: najpierw zrobie Ci rysunki Masz rysunek a)

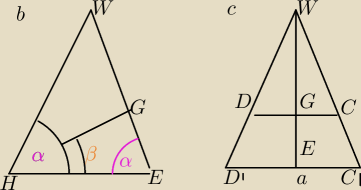
5-latek: Z rysunku a) widzisz ze ten przekroj to trapez ABCD

	1
Ptrap=		(AB+CD)*HG
	2

AB=a (to znamy z warunków zadania Do obliczenia masz HG i CD HG oblicz z trojkata HGE (rysunek b) CD oblicz z rysunku c) na razie tyle

Rok2015: Mysle ze po Nowym Roku nie zapomnisz o tym zadaniu

Metis: Nie zapomnę 5−latku

5-latek: Ciesze się bardzo Dotarla do ciebie ksiazka Geometria trojkata ?

Metis: Witaj 5−latku Jeszcze nic nie dotarło.