Funkcja dwóch zmiennych - zadania
123:
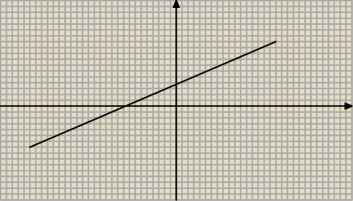
Wyznaczyć dziedzinę funkcji:
f(x,y) =
√x−2y+4
27 gru 22:26
bezendu:
x−2y+4≥0
−2y≥−x−4 / (−2)
Narysuj i po problemie.
27 gru 22:31
123: No to narysowałem wyżej

27 gru 22:32
123: co trzeba zakreskowac?
27 gru 22:33
bezendu:
Nie. To co narysowałeś wyżej to prosta, a nie zaznaczyłeś obszaru.
27 gru 22:34
bezendu:
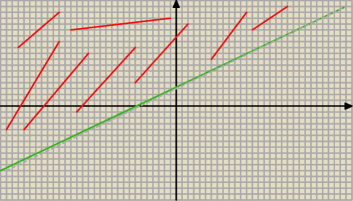
Trzeba zakreskować to co nad prostą.
27 gru 22:34
123:
27 gru 22:36
123: ta?

27 gru 22:36
bezendu:
Tak.
27 gru 22:37
123: i oczywiscie prosta jest przerywana, tak?

27 gru 22:37
bezendu:
Przerywana ? Niby czemu ?
27 gru 22:40
Metis: Nie.
27 gru 22:40
123: 
27 gru 22:42
Metis: Punkty z prostej należą do dziedziny.
27 gru 22:42
Benny: Wydaje mi się że chodzi o obszar pod prostą

27 gru 22:45
123: next

f(x,y) = √{y−x
2} + 4log
2(4−y)
y−x
2 ≥0 ⇒
x ≤√y
x ≥ − √y
oraz
y <4
27 gru 22:45
bezendu:
To teraz to narysuj i zaznacz część wspólną, ja już uciekam do swojego projektu.
27 gru 22:47
123: ups, zle zapisalem.. zaraz narysuje

27 gru 22:48
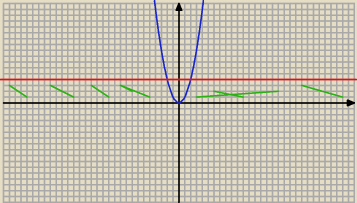
123: y> x2
y < 4
27 gru 22:51
123:
27 gru 22:56
123: tak?
27 gru 22:56
Jack: dlaczego w pierwszym podpunkcie nad prosta
skoro
y ≤ ta prosta
27 gru 22:56
123: hmm
27 gru 22:59
Metis: Przecież Benny już to napisał...
27 gru 23:04
123: Metis, 22;56 ok czy źle?
27 gru 23:06
Metis: Wyciągnij wnioski z postu Benny'ego
27 gru 23:07
123: To teraz to narysuj i zaznacz część wspólną
27 gru 23:08
123: Czy o ktory Ci chodzi?
27 gru 23:08
Mila:
Dziedzina funkcji:
f(x,y) =
√x−2y+4
x−2y+4≥0⇔
x+4≥2y
| | 1 | | 1 | |
y≤ |
| x+2 punkty płaszczyzny poniżej prostej y= |
| x+2 i na prostej |
| | 2 | | 2 | |
27 gru 23:13
Jack: wiedzialem ! ;x
27 gru 23:14
123: Mila, a drugi przykład?

27 gru 23:15
Mila:
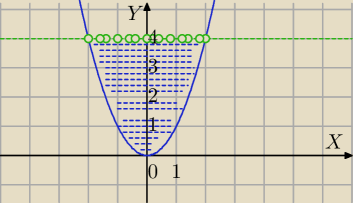
Dziedzina:
f(x,y) =
√y−x2 + 4log
2(4−y)
y−x
2≥0 i 4−y>0⇔
y≥x
2 ( punkty nad wykresem y=x
2 i na wykresie) i 4>y ( punkty poniżej prostej y=4)
27 gru 23:19
Jack: | | 2y | |
wynik to |
| w kazdym razie... |
| | x3 | |
27 gru 23:23
123: dzięki

27 gru 23:23
Jack: sorry , nie ta karta...
27 gru 23:23
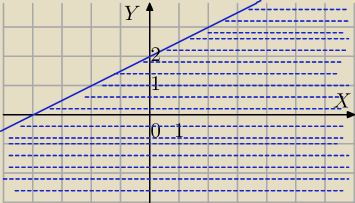
123:
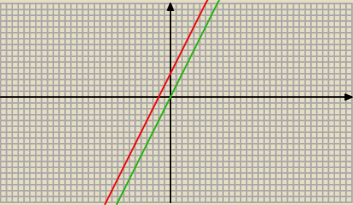
Mila, ostatni przykład

Dziedzina:
y−2x ≥0
y ≥ 2x i y−2x−4 ≠0
y ≠ 2x+4
Czyli będzie nad wykresem zielonym z wyłączeniem wykresu czerwonego(kreskuje)
ta?
27 gru 23:32
cos tam:
tak ( tylko razem z wykresemy y = 2x )
27 gru 23:36
123: tak

27 gru 23:37
123: dzięki wielkie :0
27 gru 23:38
123:
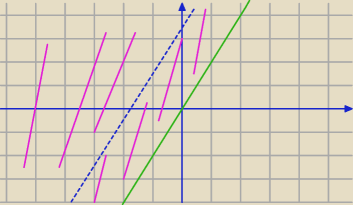
tak?
27 gru 23:40
cos tam:

27 gru 23:42
123: Ale rysować to rysuje przepieknie

27 gru 23:42
cos tam:

27 gru 23:44
 Wyznaczyć dziedzinę funkcji:
f(x,y) = √x−2y+4
Wyznaczyć dziedzinę funkcji:
f(x,y) = √x−2y+4






 f(x,y) = √{y−x2} + 4log2(4−y)
y−x2 ≥0 ⇒
x ≤√y
x ≥ − √y
oraz
y <4
f(x,y) = √{y−x2} + 4log2(4−y)
y−x2 ≥0 ⇒
x ≤√y
x ≥ − √y
oraz
y <4


 Dziedzina funkcji:
f(x,y) = √x−2y+4
x−2y+4≥0⇔
x+4≥2y
Dziedzina funkcji:
f(x,y) = √x−2y+4
x−2y+4≥0⇔
x+4≥2y

 Dziedzina:
f(x,y) = √y−x2 + 4log2(4−y)
y−x2≥0 i 4−y>0⇔
y≥x2 ( punkty nad wykresem y=x2 i na wykresie) i 4>y ( punkty poniżej prostej y=4)
Dziedzina:
f(x,y) = √y−x2 + 4log2(4−y)
y−x2≥0 i 4−y>0⇔
y≥x2 ( punkty nad wykresem y=x2 i na wykresie) i 4>y ( punkty poniżej prostej y=4)

 Mila, ostatni przykład
Mila, ostatni przykład 

 tak?
tak?


