parametr
xxxy: Dla jakich wartosci parametru k równanie
|x2−4x+3|−k+1=0
ma 4 rozne rozwiazania?
27 gru 19:47
===:
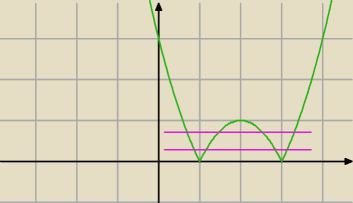
0<k−1<1
27 gru 19:52
5-latek:
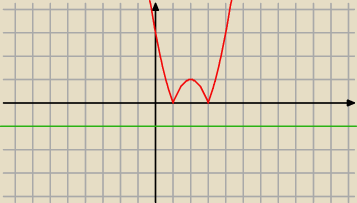
Inaczej to można zapisac
|x
2−4x+3|= k−1
Można to rozwiazc graficznie
rysując wykres y=|x
2−4x+3| i y= k−1
cztery rozne rozwiązania masz w przedziale y∊(0,1) wiec k∊(1,2)
27 gru 19:55
Eta:
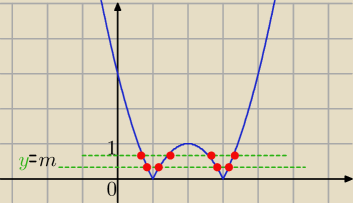
|x
2−4x+3|= k−1
f(x)=|x
2−4x+3|
y=m= k−1
dla (k−1)∊(0,1) są cztery różne rozwiżzania
k−1>0 i k−1<1 ⇒ .......... dokończ
27 gru 19:57
Eta:
.... tacy "głodni" po Świętach?

27 gru 19:58
===:
"wyposzczeni"

27 gru 20:00
Eta:
A
π... zostało ? czy też zabrakło?

27 gru 20:01
===:
jeszcze "dojrzewa" ... jest "że....."
27 gru 20:03
5-latek: nicha

27 gru 20:05
===:
... ej ...
"małolat" ... dla Ciebie to jeszcze lemoniada

27 gru 20:17
Eta:
Coś za długo ten "małolat" siedzi w przedszkolu

Blokuje miejsce ...... a może zakochał się w Pani .....

27 gru 20:19
5-latek: Eta 
To drugie

27 gru 21:05
prosta:
a gdyby w treści nie umieszczono słów " 4 różne rozwiązania"
tylko " 4 rozwiązania" to zmieniłoby coś w odpowiedzi? mam tutaj wciąż wątpliwości
jak to interpretować

27 gru 21:09
prosta:
gdy rysuję wykres liczby rozwiązań równanie to "4 różne rozw." i "4 rozw." traktuję tak samo
27 gru 21:12
 0<k−1<1
0<k−1<1
 Inaczej to można zapisac
|x2−4x+3|= k−1
Można to rozwiazc graficznie
rysując wykres y=|x2−4x+3| i y= k−1
cztery rozne rozwiązania masz w przedziale y∊(0,1) wiec k∊(1,2)
Inaczej to można zapisac
|x2−4x+3|= k−1
Można to rozwiazc graficznie
rysując wykres y=|x2−4x+3| i y= k−1
cztery rozne rozwiązania masz w przedziale y∊(0,1) wiec k∊(1,2)
 |x2−4x+3|= k−1
f(x)=|x2−4x+3| y=m= k−1
dla (k−1)∊(0,1) są cztery różne rozwiżzania
k−1>0 i k−1<1 ⇒ .......... dokończ
|x2−4x+3|= k−1
f(x)=|x2−4x+3| y=m= k−1
dla (k−1)∊(0,1) są cztery różne rozwiżzania
k−1>0 i k−1<1 ⇒ .......... dokończ





 Blokuje miejsce ...... a może zakochał się w Pani .....
Blokuje miejsce ...... a może zakochał się w Pani ..... 
 To drugie
To drugie 
