minimum i maximum lokalne ktoś:

x3
x−2

czy posiada minimum i maximum lokalne?

	2x3−6x2
pochodna wyszła mi:
	(x−2)2

funkcja rosnąca (−∞,0) funkcja rosnąca (0,2) funkcja rosnąca (2,3) funkcja malejąca (3,∞) znak dodatni przy najwyższej potędze więc zaczynamy wykres od góry, odbija się na 0 i na 2 ponieważ pierwiastek wielomianu parzysty. Proszę jeszcze o pomoc czy posiada minimum i maksimu i o wyjaśnienie abym zrozumiała. Jeśli jakiś błąd popełniłam też proszę o sprostowanie.

Jack: Naturalnie posiada Maximum lokalne w zerze i minimim w trojce

ktoś: ok dziękuję bardzo, tylko nie bardzo rozumiem, min ponieważ zmienia znak z dodatniego na ujemny, a przy zerze? cały czas jest dodatni, chyba że coś źle rozumuje. Proszę wytłumacz jeśli możesz

Jack: Funkcja

	2x3 − 6x2
y =
	(x−2)2

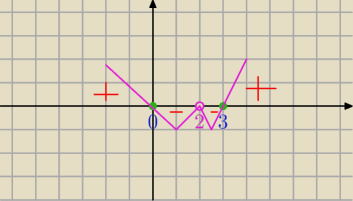
przyrownuje do zera, wiec zapisuje jako (2x³ − 6x²)(x−2)² = 0 wiem ze x ≠ 2 to tak mniej wiecej wyglada + tam gdzie wykres nad osia, minus gdzie pod osia jak widzisz w zerze jest zmiana znaku z + na minus wyobraz sobie ze idziesz do góry (+) dochodzisz do szczytu i potem schodzisz (−), oznacza to ze miedzy + a minus byłes na szczycie góry, czyli na maxie w trójce masz minus a potem plus dlatego najpierw schodzisz (−), jestes na samym dole i potem wchodzisz (+). czyli pomiedzy − a + byles na samym dole czyli minimum

Jack: mam nadzieje ze wiesz ze jak przyrownujesz do zera jakis ulamek np.

x2
(x−3)2

to zapisujesz to w "rownowaznej postaci wielomianowej" czy jakos tak : D czyli x²(x−3)² oczywiscie mozesz zapisac samo x², ale wtedy musisz pamietac ze ta 3 jest wylaczona z dziedziny. Ja wole zawsze zrobic ta rownowazna postac i po prostu zrobic otwarte koleczko w tej trojce a ze np. (x−3)² jest do kwadratu...to odbijam od osi. Najprawdopodobniej ta funkcja ma asymptote ukosna, ale mniejsza o to : D

ktoś: a czemu przez zero przechodzi, a nie odbija się? (2x³−6x²)(x−2)²=0 czyli x²(2x−6)(x−2)²=o tu myślała że w związku z tym, że pierwszy wielomian jest w parzystej potędze czyli zero to się odbije.

Jack: O kurcze faktycznie przepraszam ...nie zauwazylem Naturalnie w zero sie odbija

ktoś: ok, to proszę w takim razie powiedz mi co teraz z maksimum? i minimum?

ktoś: Proszę Jack, albo może ktoś inny, czy ma wtedy ma tylko minimum w trójce?

ktoś: a maksimum nie ma

utem: D: x≠2 x=2 asymptota pionowa f'(x)=0⇔2x³−6x²=0 i x≠2 2x²*(x−3)=0 x=0 pierwiastek podwójny, lub x=3 f'(x)≥0⇔ x²*(x−3)≥0 przy przejściu przez x=3 pochodna zmienia znak z ujemnego na dodatni ( maleje, rośnie)⇔ dla x=3 funkcja f(x) ma minimum f(3)=27

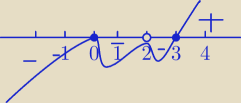
ktoś: a czemu od dołu zacząłeś, nie powinno iść od góry, znak przy najwyższej potędze jest dodatni?

utem: Zaczynamy z prawej i jest od góry.

ktoś: ok teraz rozumiem, dziękuję bardzo

Mila:

Jack: Wróciłem... Jak jeszcze hakies pytania to smialo

ktoś: to jeśli możesz to potrzebuję jeszcze punkt przegiecia. Powinnam obliczyć drug pochodną i co dalej?

Jack: heh, zazwyczaj tego nie liczylem bo nigdy nie bylo mi to potrzebne... aczkolwiek druga pochodna mowi o punkcie przegiecia przyrownujesz druga pochodna do zera...

ktoś: ok, dziękuję

Jack: oczywiscie to jeszcze nie wszystko po przyrownaniu do zera otrzymujesz jakis x... robisz f '' (od jakiejs wartosci z lewej strony i potem z prawej) i musza miec rozne znaki zeby byl taki punkt

Jack: np. powiedzmy ze Ci druga pochodna wyszla f '' (x) = 2x 2x = 0 x =0 sprawdzasz z lewej strony zera jakakolwiek liczbe np. −2 f '' (−2) = −4 teraz z prawej strony zera np. 3 f '' (3) = 6 widzimy ze z lewej strony jest minus (−4) z prawej + (+6) takze istnieje punkt przegiecia z wkleslej na wypukla : D

Jack: wspolrzedne tego punktu, skoro ci wyszlo ze jest przegiecie dla x= 0 to liczysz f(0) = jakaś liczba (napiszę Y) i wtedy twoj punkt to (0,Y) −>> podstawiasz do funkcji , nie do pochodnej, ani nie do drugiej pochodnej w tym wypadku co napisalem

Jack: w tym wypadku co napisalem ten punkt wynosi (0,Y) hehe, nie dokonczylem mojego zdania : D

ktoś: ok dziękuję Tobie zrobiłam, jeszcze raz dziękuję za pomoc.

ktoś: troche mi to zajęło, ale z pomocą zawsze lepiej

Jack: