Pierwiatki magdaC: Obliczyć pierwiastki stopnia 3 z liczby:

(1−i)7
(1+i)3

magdaC: Pomógłby ktoś?

zeesp: (1+i)²=1+2i−1=2i więc (1+i)³=2i(1+i)=−2+2i=−2(1−i) (1−i)²=−2i (1−i)⁶=(−2i)³=−8i³=−8*i²*i=8i (1−i)⁷=8i(1−i) zatem

(1−i)7		8i(1−i)
	=		=−4i
(1+i)3		−2(1−i)

Sprawdz czy sie nie pomyliłem... a z tego juz łatwo

piotr: (1−i)⁷=8(1+i) (1+i)³=2(−1+i)

1+i		√2ei π4
	=		=e−i π=−i
−1+i		√2e−i 3π4

czyli ³√−4i=³√4e^iπ₂ lub ³√−4i=³√4e^−iπ₆ lub ³√−4i=³√4e^−i5π₆

magdaC: Dziękuje

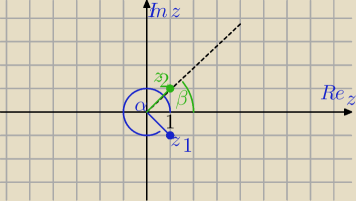utem: z₁=1−i |z₁|=√2

	7π
α=
	4

|z₂|=√2

	π
β=
	4

	7π   7π   √27*[cos(7* )+i sin(7* )]   4   4
z=		=
	π   π   √23*[cos(3* )+i sin(3* )]   4   4

	49		3		49		3
=√24*cos((		−		)*π)+i sin((		−		)*π)=
	4		4		4		4

	3π		3π
=4*cos(		+i sin		)=−4i
	2		2

³√−4i |−4i|=4

	3π
φ=
	2

	3π   +2kπ   2		3π   +2kπ   2
3√−4i=3√4*(cos		+i sin		) gdzie k=0,1,2
	3		3

	π		π
z0=3√4*(cos		+i sin		)=3√4*i
	2		2

	7π		7π		√3		1
z1=3√4*(cos		+i sin		)=3√4*(−		−		i)
	6		6		2		2

	11π		11π		√3		1
z2=3√4*(cos		+i sin		)=3√4*(		−		i)
	6		6		2		2

=================================