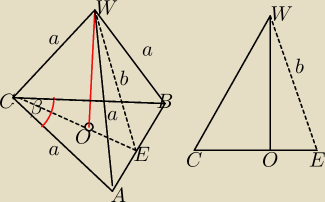
Ostroslup 5-latek: Czesc Metis mam dla Ciebie zadanko ze stereometrii (bardzo fajne ) Tresc : W ostrosłupie trojkatnym wszystkie krawędzie boczne i dwa boki podstawy sa rowne (a) Kąt miedzy równymi bokami podstawy jest rowny β (nie dalem α żeby się nie zlewalo a a ) Oblicz objetosc i pole całkowitej powierzchni ostrosłupa uwazajac a i β za waidome . Obliczona powierzchnie i objetosc doporowadzic do postaci logarytmowanej i podac warunki rozwiązalności zadania Rysunek do zrobienia samemu . Powodzenia

Metis: Cześć 5−latku Dzięki Gdy będę miał rozwiązanie to je tutaj przedstawię.

5-latek: Ok

Jack: kto wymysla takie zadania

Jack: Jeszcze to nie jest ani ostroslup prosty ani prawidlowy...to jestem bardzo ciekaw gdzie jest jego wierzcholek...chyba nad jednym z wierzcholkow podstawy trojkata...

Kacper: Dokładnie wiadomo, gdzie jest spodek wysokości tego ostrosłupa. Myśl

5-latek:

5-latek: Zapomnialem oznaczyć wysokość (h) ale to nie powinien być problem

5-latek: Metis mam prosbe Zrob zdjęcia spisu treści Modenowa i prześlij na forum dla Bennego . dzięki

Metis: Nie ma sprawy Już robię.

5-latek: Pomoge CI przy polu całkowitym Wszystkie krawędzie oprócz AB maja dlugosc a . Nie zmamy dlugosci krawędzi AB Sciana boczna ABW jest przystajaca do podstawy ABC i kazda z nich ma pole P_ΔABW= P_ΔABC=0,5a²*sinβ Pozostale dwie sciany boczne sa jak widzisz przystającymi trójkątami o rownych krawędziach wiec będą to jakie trojkaty ? wiec P_ΔACW= P_ΔBCW = ile te pola wynoszą ? Dodajesz wszystkie pola i masz pole całkowite ostrosłupa najpierw policz ile to pole wynosi

5-latek: No i co Jack widzisz już jaki będzie trojkat w podstawie ?

Jack: szczerze? nie czytalem do konca polecenia wiec nwm

5-latek: Wiec przy okazji przeczytaj i spróbuj rozwiazac zadanie

5-latek: I jak Metis idzie zadanko ?

Eta: Czy taka jest odpowiedź:

	1
V=		a3sinβ2*√sin(60o+β2)*sin(60o−β2 , β∊(0o,120o)
	6

Jack: Eta wszystko obliczy

5-latek: Eta

	1		1
W odpowiedzi mam na początku		a nie		po sprowadzeniu do postaci
	3		6

logarytmowalnej i kąt tez się zgadza

Eta: Pewnie gdzieś po drodze "zgubiłam" dwójkę

5-latek: Jack tenostroslup jest prosty bo ma wszystkie rowne krawędzie boczne . Ma w podstawie trojkat równoramienny i to będzie wazna wiadomość do policzenia pola podstawy Dokoncze to zadanie Pozostale dwie sciany sa trójkątami równobocznymi i kazda z nich ma pole rowne U{1}}{4}a²√3 wiec pole powierzchni całkowitej tego ostrosłupa wynosi

	1		1		√3
Pc= 2*		sin2β+2*		a2√3= a2(sinβ+		)
	2		4		2

==================================================

	√3
(sinα+		}) doprowadzimy do postaci logarytmowanej
	2

	β+60o		β−60o
= sinβ+sin60o= 2sin		cos		= 2sin(30o+β/2)cos(30o−β/2)
	2		2

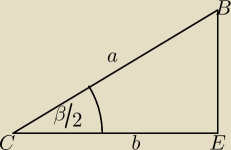
Teraz obliczmy objetosc ostrosłupa Potrzebna wysokość WO=h jest także wysokoscia trojkata WCE wiec

	PΔWCE		PΔWCE		2PΔWCE
h=		=		=
	0,5CE		0,5b		b

b=c*cosβ/2 Natomiast P_Δ WCE ze wzoru Herona P_ΔWCE=√p(p−a)(p−b)(p−b)= (p−b)√p(p−a)

	a
p=0,5(a+b+b)=		+b
	2

	a
p−a= b−
	2

	a
p−b=
	2

	a		a		1		a
PΔWCE= 0,5a√(		+b)(b−		)=		a√b2−(		)2
	2		2		2		2

	2PΔWCE		a		a
h=		=		*√b2(		)2
	b		b		2

Podstawiamy b do wzoru i mamy

	a		1
h=		*√cos2β/2−
	cosβ/2		4

Liczymy objetosc

	1
V=		*PΔABC*h
	3

	1		1		a		1
V=		*		a2sinβ*		*√cos2β/2−		=
	3		2		cosβ/2		4

1		2sinβ/2cosβ/2		1		1
	a3		*√cos2β/2−		= U{1}[3a3sinβ/2*√cos2β/2−
6		cosβ/2		4		4

Można wyrażenie pod pierwiastkiem sprwadzic do postaci logarytmowanej

	1
cos2β/2−		= (cosβ/2−0,5)(cosβ/2+0,5)= (cosβ/2−cos60o )(cosβ/2+cos60o )=
	4

= −2sin(β/4+30^o)(sinβ/4−30^o)*2cosβ/4+30^o)(cosβ/4−30^o)= Teraz łączymy 1 z 3 i 2 z 4 wtedy = −sin(β/2+60^o)(sinβ/2−60^o)= sin(60^o+β/2)(sin(60^o−β/2)

	1
to V=		a3sinβ/2*√sin(60o+β/2)sin(60o−sinβ/2)
	3

=============================================

5-latek: Trraz żeby ten wzor na objetosc nie stracil sensu wyrażenie pod pierwiastkiem musi być dodatnie Pierwszy czynnik jest dodatni na pewno bo β jako kąt w trójkącie spelnia nierownosc 0^o<β<180^o wiec 0^o<β/2<90 60^o<60^o+β/2<150 sin(60^o+β/2)>0 należy zbadac czynnik drugi Musi tez być dodatni Z nierownosci 0^o<β/2<90 ^o mamy ze 0^o>−β/2>−90 ^o dodajemy 60⁰ do wszystkich stron nierownosci 60⁰>60^o−β/2>−30 Ztego widzimy ze sin(60^o−β/2) może być ujemny wiec należy zazadac aby 60^o−β/2>0^o to b<120^o czyli widać ze dla kątow ≥120^o nie da rady zbudować czworościanu o 5 krawędziach rownych Ja miałem takie zadanie na maturze

Metis: 5−latku ciekawe to zadanie

5-latek: Prawda No to masz takie Trapez równoramienny ma posdtawy a,b i a>b jakie powinno być ramie p i wysokość h tego trapezy aby można było wpisac wen okrag ?

Jack: 5−latek? mature pisal? : D

5-latek: Bledy poprawisz

Benny: Przejezyczyl sie. Pewnie chodzilo o Pania przedszkolanke

5-latek: Tak Jack pisal Pani z przedszkola mi kazala a co powie Pani to święte

Metis: Jack jak 5−latek może pisać maturę ? Co to za pytanie