Logika
Benny: Mila,
Saizou,
Eta,
: ), ktoś z Was będzie miał chwilkę czasu poświęcić na
logikę(mój ulubiony przedmiot)?

26 gru 22:04
Saizou : Ja będę mieć, ale tak kolo 17 dopiero.
27 gru 14:16
Benny: Ok, ja możliwe, że też będę wtedy

27 gru 14:42
Saizou :
a co konkretnego czy tak ogólnikowo ?
27 gru 15:15
Saizou :
prawdopodobnie będę dzisiaj o 17, a jak nie to jutro na 100% (w sumie to jutro cały dzień)
27 gru 15:21
Benny: Pokaż, że zbiory ℕ i ℕk dla pewnego, ustalonego k∊ℕ są równoliczne i skonstruuj odpowiednią
bijekcję.
27 gru 18:15
27 gru 19:57
Benny: Nie ogarniam jak oni te funkcje definiują.
27 gru 20:23
Benny: Jest na to jakiś sposób czy trikowo?
27 gru 23:39
Saizou :
na razie nie mam pojęcia

jak coś wykombinuję to dam znać xd
28 gru 10:12
Benny: ok

28 gru 11:29
Saizou :
to taka luźna propozycja
można pokazać że N~N2
skorzystać z faktu że jeśli A1~B1 oraz A2~B2 to A=A1 x A2~B1 x B2=B
i powtarzając tę czynność k razy mamy pokazane że Nk~N
28 gru 12:00
zombi: Żeby pokazać, że ℕ∼ℕ
2, wystarczy to zrobić jak dla liczb wymiernych.
W przypadku liczb wymiernych pisaliśmy je w "tablicy" w takiej postaci
.
.
.
| | 1 | | 1 | | 2 | | 3 | | 2 | | 1 | |
Szliśmy po przekątnych |
| → |
| → |
| → |
| → |
| → |
| ... |
| | 1 | | 2 | | 1 | | 1 | | 2 | | 3 | |
Dowód na równoliczność N i N
2 robimy analogicznie tylko 1. nie wykreślamy powtarzających się
liczb,
2. nie rozpatrujemy ułamków tylko pary uporządkowane.
Więc będziemy iść
<1,1> → <1,2> → <2,1> → <3,1> → <2,2> → <1,3> ...
Równoliczność dla N
k pokazujemy przez prostą indukcję.
28 gru 12:41
Benny: Nie wiem czy takie wypisanie coś da, myślę, że to musi być dowód formalny.
28 gru 14:41
28 gru 15:03
zombi: Czasami znalezienie odpowiedniej bijekcji wcale nie jest takie proste, więc wykorzystuje się
metodę przekątniową albo tw. Cantora−Bernsteina.
28 gru 15:06
Benny: To jest tak trochę nieintuicyjne. Układamy liczby wymierne w nieskończony ciąg i mówimy, że
jest on przeliczalny.
28 gru 15:16
28 gru 23:10
fffff:
f(x,x) → x
2
f(x,y), x<y → y
2−x+1
f(x,y), x>y → (x−1)
2+y
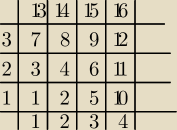
W tabelce jest kolejność par uporządkowanych, na podstawie której tworzone są funkcje.
Oczywiście ta tabelka to tylko fragment, żeby pokazać zasadę porządkowania.
Powyższy zapis to dowód dla ℕ ~ ℕ
2
Dla ℕ ~ ℕ
k będzie funkcja:
f
k(a
1,a
2,...,a
k)=f
2(f
k−1(a
1,a
2,...,a
k−1),a
k)
O to chodziło w tym zadaniu?

29 gru 00:42


 jak coś wykombinuję to dam znać xd
jak coś wykombinuję to dam znać xd

 Zbiór jest przeliczalny, jeśli jego elementy możemy ustawić w ciąg. Jeśli mi nie wierzysz to
może prof. Newelskiemu uwierzysz
https://www.math.uni.wroc.pl/~newelski/dydaktyka/wdm-A/skrypt3/skrypt/node12.html
Przykład 2. prawie na samym dole.
Zbiór jest przeliczalny, jeśli jego elementy możemy ustawić w ciąg. Jeśli mi nie wierzysz to
może prof. Newelskiemu uwierzysz
https://www.math.uni.wroc.pl/~newelski/dydaktyka/wdm-A/skrypt3/skrypt/node12.html
Przykład 2. prawie na samym dole.
 f(x,x) → x2
f(x,y), x<y → y2−x+1
f(x,y), x>y → (x−1)2+y
W tabelce jest kolejność par uporządkowanych, na podstawie której tworzone są funkcje.
Oczywiście ta tabelka to tylko fragment, żeby pokazać zasadę porządkowania.
Powyższy zapis to dowód dla ℕ ~ ℕ2
Dla ℕ ~ ℕk będzie funkcja:
fk(a1,a2,...,ak)=f2(fk−1(a1,a2,...,ak−1),ak)
O to chodziło w tym zadaniu?
f(x,x) → x2
f(x,y), x<y → y2−x+1
f(x,y), x>y → (x−1)2+y
W tabelce jest kolejność par uporządkowanych, na podstawie której tworzone są funkcje.
Oczywiście ta tabelka to tylko fragment, żeby pokazać zasadę porządkowania.
Powyższy zapis to dowód dla ℕ ~ ℕ2
Dla ℕ ~ ℕk będzie funkcja:
fk(a1,a2,...,ak)=f2(fk−1(a1,a2,...,ak−1),ak)
O to chodziło w tym zadaniu? 