Zbadaj zbieżność szeregu
student: Zbadaj zbieżność szeregu:
26 gru 20:12
sushi_gg6397228:
ogranicz cosinusa
| | 1 | |
i ∑ a* |
| − co możesz o nim powiedzieć ? |
| | n | |
26 gru 20:13
student: Ten drugi jest rozbieżny
26 gru 20:16
sushi_gg6397228:
wiecTwoj jest...
26 gru 20:20
student: czyli jeżeli jeden szereg jest ograniczony a drugi rozbieżny to ich iloraz też?
26 gru 20:21
student: Tzn iloczyn*
26 gru 20:22
sushi_gg6397228:
czytaj moj wpis o 20.13 i wykonaj polecenie
wpis o 20.21 nie dotyczy tego
26 gru 20:24
student:
| 1 | |
| jest rozbieżny, ale w tym przypadku nie mówi nam to nic o szukanym szeregu |
| n | |
26 gru 20:26
sushi_gg6397228:
a ograniczenie dolne cosinusa istnieje ?
26 gru 20:27
student: | | 1 | |
czyli szereg będzie >− |
| |
| | n | |
Ok, już rozumiem, dzięki
26 gru 20:28
sushi_gg6397228:
| | 1 | |
∑ |
| szereg ograniczony , kazdy element siedzi w przedziale (0; 1> |
| | n4 | |
| | 1 | | 1 | |
∑ |
| * |
| szereg zbieżny− czyli Twój wpis o 20.21 obalony |
| | n4 | | n | |
26 gru 20:29
student: A co jeśli cosinus byłby do potęgi 2?
26 gru 20:30
sushi_gg6397228:
dajesz w dolu i góry i tw o 3 ciagach
nawet mozna by bylo sie uprzeć ze
| | 1 | |
cos 1 < cos |
| bo cosinus jest malejący ( patrz wykres) |
| | n | |
na zdrowie
26 gru 20:31
sushi_gg6397228:
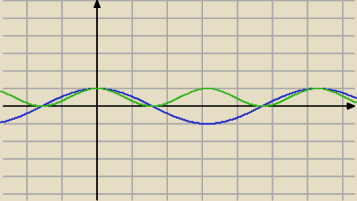
cosinus w potedze drugiej <0; 1> patrz wykres
26 gru 20:33