mindfuck
piniondze: Ile pierwiastków ma wielomian w(x) = x3 − x2 − 2x + 1 w przedziale (−2,2) ?
25 gru 18:40
piniondze: haloo
25 gru 19:12
Jerzy:
1) twierdzenie Bolzano
2) pokaż ,że funkcjs rośnie w całej dziedzinie
25 gru 19:13
wmboczek: funkcja nie rośnie w całej D
chyba trzeba pochodne i wartości funkcji w pkt zerowania pochodnej
25 gru 19:19
piniondze: tzn? poziom LO
25 gru 19:20
piniondze: nooo ale co dadzą te wartosci? mozna MNIEJ WIĘCEJ okreslic ile funkcja ma pierwiastków jezeli
sobie naszkicujemy jej wykres z przebiegu zmiennosci, ale czy jakos inaczej tez mozna?
25 gru 19:22
piniondze: a czy mozna jakos wyliczyc te pierwiastki?
25 gru 19:22
5-latek : twierdzenie Sturma
25 gru 19:23
Jack: w(x) = x(x−2)(x+1) + 1
ale to nic nam nie da...
25 gru 19:24
piniondze: No coż, zawsze pozostaje mi podstawienie kilku wartości z podanego przedziału i szkic :v
25 gru 19:30
piniondze: Trochę barbarzyńsko, ale co tam.
25 gru 19:31
Jack:
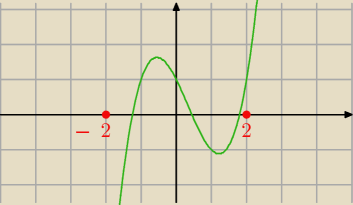
25 gru 19:32
piniondze: no dokladnie

25 gru 19:33
Jack: innego sposobu jak ekstrema nie widze...
mozesz obliczyc lim −2 z prawej strony i lim 2 z lewej...
oraz pochodna i te ekstrema
25 gru 19:36
ICSP: f(−2) . f(−1) . f(0) , f(1) . f(2) i liczyć na szczęście

25 gru 19:45
prosta:
Twierdzenie Darboux (O przyjmowaniu wartości pośrednich)
Jeżeli funkcja f jest ciągła w przedziale domkniętym <a, b> oraz:
− f(a) < f(b),
− p ∈ (f(a), f(b)),
to istnieje taki punkt c ∈ (a, b) dla którego f(c) = p.
25 gru 19:53


