wielomiany xxxy: Rozważamy wielomian W(x)=(p²+1)x² +2(p²+p)x + p²+2p−1 wyznacz wszystkie wartosci parametru p dla ktorych w(x) ma dwa pierwiastki x1 i x2 spelniajace warunek x1<1<x2

zzz: Δ

xxxy: Δ=(2p−2)² pierwiastek z delty mam 2p−2 wyliczyłam miejsca zerowe ale podstawiajac do nierownosci wychodzi mi sprzecznosc

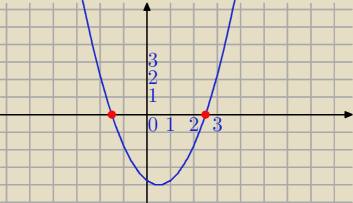
tx: 1) a=p²+1>0 parabola skierowana do góry 2) Δ>0 istnieją dwa różne pierwiastki 3) f(1)<0 sytuacja jak na rysunku.

Jack: Δ = (2p² + 2p)² − 4(p²+1)(p²+2p−1) po uproszczeniu Δ = 4(p²−2p+1) czyli Δ = 4(p−1)²

wmboczek: Kolejność x₁ i x₂? Jeden z pierw to −2 a drugi >1

Kacper: Wystarczy warunek f(1)<0.