matematykaszkolna.pl
trygonometria: few: kąt α jest kątem ostrym oraz tgα=3. Oblicz wartość wyrażenia:
sin3α+cos2αsinα−√3cosα 
cosα+√3sinα 
25 gru 09:26
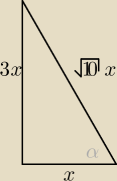
Saizou : rysunek skoro α jest kątem ostrym to (patrz rysunek)
 3√10 
sinα=
 10 
 √10 
cosα=
 10 
podstaw i oblicz
25 gru 09:50
Jack: Albo...
sin α(sin2α + cos2 α)−√3cosα 
=
cos α+ √3sin α 
= {sin α − √3 cos α}{cos α + √3 sinα}
 sin α 
Skoro tg α = 3 to
= 3
 cos α 
Czyli sin α = 3 cos α Podstawiasz za sin te 3 cos...
25 gru 11:21
Jack: Albo...
sin α(sin2α + cos2 α)−√3cosα 
=
cos α+ √3sin α 
= {sin α − √3 cos α}{cos α + √3 sinα}
 sin α 
Skoro tg α = 3 to
= 3
 cos α 
Czyli sin α = 3 cos α Podstawiasz za sin te 3 cos...
25 gru 11:21
Jack:
sin α − √3 cos α 
cos α + √3 sinα 
Przepraszam jesli sie dwa razy wkleilo... Mi wyszlo
5√3 − 6 
14 
25 gru 11:25
naciz: Dzieki. Tez tak podatawialem ale wyszło cos innego. Jeszcze raz to ogarne.
25 gru 11:52