Uzasadnij, że pola trójkątów. Archeolog: Tak jak wszystkie inne działy które przerabiam opanowałem, tak figury geometryczne, a szczególnie trójkąty chyba doprowadzą mnie do depresji... Obrazek do zadania: http://pl.static.z-dn.net/files/d11/1b11eb3db272910c153d42e222344a53.jpg Punkt P należy do środkowej CS trójkąta ABC. Uzasadnij, że pola trójkątów APC i PBC są równe. Nie wiem jak się te wszystkie trójkąty liczy, jest pełno wzorów nie wiadomo co kiedy użyć, miliony przekształceń... tragedia. Osoba która nie umie rysować prostych figur bez linijki (na maturze ew. dowodem chyba można sobie pomagać) i nie "widzi" tych figur ma jakieś szanse w ogóle rozwiązania zadań z tymi badziewnymi trójkątami?

===: więcej wiary w siebie

===: P_ΔASC=P_ΔBSC P_ΔASP=P_ΔBSP i wszystko jasne

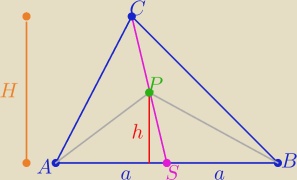" " ": Każda środkowa dzieli trójkąt na dwa trójkąty o równych polach

	a*H		a*H
dowód : P(ASC)=		i P(BSC)=		⇒ P(ASC)= P(BSC)
	2		2

	a*h		a*h
Podobnie w trójkącie APB : P(ASP)=		=P(BPS)=
	2		2

P(ASC)= P(APC)+P(ASP) i P(BSC= P(BSP)+P(BPC) i P(ASP)=P(BPS) ⇒ P(APC)=P(BPC) c.n.u

Eta: A ja kocham planimetrię

5-latek: https://www.youtube.com/watch?v=ga3QwPYq2Q0