Rachunek rozniczkowy
Kacper : Wykaż ze funkcja f(X) = x3−2x2+8x−15 ma tylko jedno miejsce zerowe. Pomocy bo nie chce mi
się liczyć wszystkich możliwości wymiernych pierwiastków tego wielomianu chyba jest inny
sposób?
23 gru 23:36
ICSP: f'(x) = 3x2 − 4x + 8 = 2x2 + (x − 2)2 + 4 > 0 ⇒ f jest rosnaca. □
23 gru 23:39
Jack: x(x(x−2) + 8)−15
23 gru 23:43
Kacper : Co to da
23 gru 23:47
ICSP: też nie wiem, ale
Jack pewnie wyjaśni
23 gru 23:53
Kacper : A co da to ze jest rosnąca hmm?
23 gru 23:59
Kacper : Bo narazie nie rozumiem zadania
24 gru 00:00
Jack: napisalem dokladnie to co ICSP , w sensie (x−2) w nawiasie...
wlasciwie to nie wiem co to da, ale fajnie wyglada... a widac ze funkcja rosnie bo kazdy iks
dodatni...
wiec wniosek ten sam co u ICSP
24 gru 00:01
ICSP: funkcja która jest ciągła i rosnaca może mieć maksymalnie 1 miejsce zerowe.
Dodatkowo wiemy, że wielomian stopnia III moze mieć tylko nieparzystą liczbę pierwiastków.
24 gru 00:01
Jack:
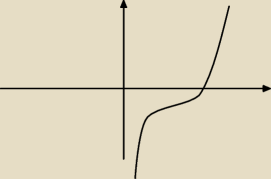
to ze ma tylko jedno miejsce zerowe ; d
24 gru 00:02
Kacper : Hiperbola −1/x tez jest rosnąca w całej dziedzinie
24 gru 00:10
Kacper : wielomian stopnia III moze mieć tylko nieparzystą liczbę pierwiastków − ciekawe stwierdzenie
ale czy jesteś w stanie je udowodnić?
24 gru 00:12
ICSP: nie jest rosnaca.
24 gru 00:12
Kacper : Jest
24 gru 00:13
Kacper : Napisałem ➖ 1/x a nie 1/x
24 gru 00:14
Jack:
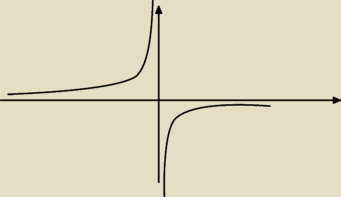
Hiperbola naturalnie nie jest funkcją ciągłą bo
np.
x nie nalezy do dziedziny
lim x−>0 + ( f(x) ) = −
∞
lim x−>0 − ( f(x) ) =
∞
Czyli funkcja nie jest ciagla...
24 gru 00:20
Jack: jak napisal ICSP
" funkcja która jest ciągła i rosnaca może mieć maksymalnie 1 miejsce zerowe "
24 gru 00:20
ICSP: | | 1 | |
Hiperbola f(x) = − |
| nie jest funkcja rosnacą. |
| | x | |
24 gru 00:37
henrys: każdy wielomian stopnia 3 ma co najmniej jedno rzeczywiste miejsce zerowe, ponieważ f jest
funkcją rosnącą ma dokładnie jedno
24 gru 00:42
henrys: wystarczy, że f jest monotoniczna
24 gru 00:43
henrys: @ICSP nie doczytałem, że napisałeś wcześniej
24 gru 00:54
Kacper : Jest rosnąca w całej swojej dziedzinie
24 gru 07:28
Kacper:
Proszę się nie podszywać pode mnie.
Na dodatek bzdury piszesz powodując obrazę tego nicku.
| | 1 | |
Funkcja y=− |
| nie jest monotoniczna w D ! |
| | x | |
24 gru 08:26
Kacper : Jest rosnąca w każdym z przedziałów (−∞, 0),(0,+∞) czyli w swojej dziedzinie. Zupełnie nie wiem
czemu się wykłucasz
24 gru 08:54
Jack: Mozesz powiedziec, ze jest monotoniczna i rosnaca w przedziale (−∞,0)
Ale nie mozesz powiedziec, ze w calym przedziale.
Czy funkcja jest rosnaca w przedziale (−1;1)?kcja rosnąca
Funkcję f nazywamy rosnącą w zbiorze X, jeśli dla dowolnych argumentów x1, x2 ∈ X prawdziwa
jest implikacja x1 < x2 ⇒ f(x1) < f(x2)
Jesli wezmiesz minus jeden i jeden...
f(−1)= 1
f(1)= −1
Czy zatem skoro x1 < x2 to f(x1) jest mniejsze od f(x2)?
1 < − 1 ?
24 gru 10:17
Kacper:
24 gru 14:10
Kacper : Jest rosnąca w każdym z przedziałów należących do dziedziny. Nie zaprzeczam tej implikacji tym
stwierdzeniem, nie stwierdziłem ze jest rosnąca w SUMIE PRZEDZIAŁÓW co jest nieprawda.
24 gru 15:09
Jack: Stwierdzasz ze jest rosnaca...skoro jest rosnaca to musi byc monotoniczna a ona ofc
monotoniczna nie jest...mowie tu o calej dziedzinie
24 gru 15:54
Kacper:
Kacper nie rozumiesz w takim razie co piszesz.
25 gru 08:39
b.: Dodam jeszcze do postu Jacka z 24 grudnia 00:20, że −− wbrew temu co tam napisane −− funkcja
f(x)=−1/x jest ciągła.
26 gru 22:30
piotr: wielomian trzeciego stopnia może mieć parzystą ilość pierwiastków rzeczywistych, z tym że jeden
z nich jest tzw. pierwiastkiem podwójnym, np.:
ma pierwiastki: 0 jako podwójny i
32
26 gru 23:06