trojkat
Ola:
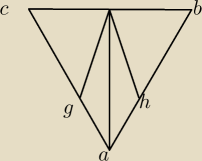
Korzystając z podanych niżej informacji, wykaż, że odcinek AD zawiera się w dwusiecznej kąta
BAC.
|BD|=|CD|
|DG|=|DH|
∡CDG=∡BDG
20 gru 21:49
cosinusx: Z założeń wynika, że trójkąty CDG i BDH są przystające (mają te same kąty i boki).
Zatem ∡GCD=∡HBD, czyli trójkąt ABC jest równoramienny.
W trójkącie równoramiennym wysokość opuszczona na podstawę dzieli ją na dwie równe części.
Ponieważ CD=BD, to odcinek AD jest wysokością trójkąta ABC.
Wysokość trójkąta równoramiennego opuszczona na podstawę jest jednocześnie dwusieczną kąta.
20 gru 22:45
Eta:
I
bingo 
20 gru 22:49
 Korzystając z podanych niżej informacji, wykaż, że odcinek AD zawiera się w dwusiecznej kąta
BAC.
|BD|=|CD|
|DG|=|DH|
∡CDG=∡BDG
Korzystając z podanych niżej informacji, wykaż, że odcinek AD zawiera się w dwusiecznej kąta
BAC.
|BD|=|CD|
|DG|=|DH|
∡CDG=∡BDG
