Proszę o podpunkt b ) Madzia: witam, bardzo proszę o rozwiązanie podpunktu b) Zadanie: Rozpatrujemy trapezy równoramienne, w których jedna z podstaw jest 3 razy dłuższa od drugiej oraz suma długości podstaw i wysokości trapezu jest równa 24 cm. a) Wyznacz długości boków trapezu, wiedząc że jego pole jest równe 64 cm² b) WYZNACZ DŁUGOŚCI BOKÓW TRAPEZU, KTÓRY MA NAJWIĘKSZE POLE. OBLICZ TO POLE a) a²−6a+8=0 Δ=4 √Δ=2 a1=2 a2=4 JAK OBLICZYĆ PODPUNKT B?

Madzia:

Eta: b) 4a+h=24 ⇒ h= 24−4a , a∊(0,6) P= 2a*h ⇒ P(a)= 2a(24−4a) = −8a²+48a −−− f. kwadratowa osiąga maximum

	−48
dla amax=		= 3 to hmax= 24−4*3= 12
	−16

P_max= 2a*h=6*12= 72 cm²

Madzia: trzeba rysować parabolę dla a∊(0,6) ?

cosinusx: a− dłuższa podstawa b− krótsza podstawa h− wysokość trapezu c− ramię trapezu a,b,c,h >0 a=3b a+b+h=24 3b+b+h=4b+h=24 h=24−4b Podstawiamy do wzoru na pole trapezu:

	(a+b)*h
P=
	2

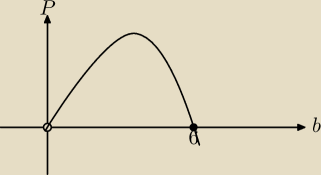
P=U{{4b*(24−4b)}{2} P=2b(24−4b) P=48b−8b² −otrzymaliśmy funkcję kwadratową, gdzie zmienną jest b Przyrównujemy sobie do zera: 48b−8b²=0 /:8 6b−b²=0 b(6−b)=0 b₁=0 b₂=6 −pierwiastki (miejsca zerowe) naszej funkcji kwadratowej Rysujemy sobie oś lub układ współrzędnych, zaznaczamy nasze pierwiastki. Funkcja jest funkcją kwadratową, czyli wykres to parabola. Współczynnik przy b² jest ujemny, czyli ramiona paraboli skierowane są w dół. Z rysunku łatwo odczytać, że funkcja− czyli pole− przyjmuje największą wartość w wierzchołku paraboli. Wzór na pierwszą współrzędną wierzchołka paraboli:

	−B
b=		, gdzie A,B to współczynniki funkcji kwadratowej P(b)=Ab2+Bb+C
	2A

	−6
Zatem b=		=3 >0 (zgodność za założeniami)
	−2

a=3b=9 h=24−4b=24−12=12 c obliczymy z tw. Pitagorasa.

	a−b
x=		=3
	2

c²=x²+h² c²=9+144=153 c=√153

Eta:

	−b
Dla f(x)=ax2+bx+c , xmax=
	2a

to dla paraboli ( chińskiej)

	−48
P(a)= −8a2+48a , amax=		= 3
	2*(−8)

Eta: Omg aleś się cosinusku opisał

Madzia: Dziękuję wam!