stozek opisany na kuli stozek: Na danej kuli opisać stożek o najmniejszej objętości. Prawdopodobnie trzeba jakąś granicę policzyć albo coś takiego? Z góry dzięki za pomoc

stozek: I jeszcze potrzebuję pomocy z tym zadaniem: Wykazać, że funkcja jest stała:

	x
f(x)=arctgx−arcsin		, x∊R
	√x2+1

stozek: Pomoże ktoś przynajmniej od czego zacząć?

zeesp: ile wynosi f'(x)

stozek: tak myślałem, że pochodną trzeba będzie liczyć, zaraz postaram się to zrobić, dzięki, a to pierwsze?

stozek:

	1−(x2+1)√x2+1
pochodna mi wyszła dziwna strasznie, pewnie coś źle jest
	x2+1

stozek: ma ktoś jakikolwiek pomysł na pierwsze?

PW: Tak, prawdopodobnie trzeba policzyć ekstremum pewnej funkcji, czy coś takiego.

Mila:

	x
(arcsin(		))'=
	√x2+1

	1		x
=		*(		)'=
	√1−(x2)/(x2+1)		√x2+1

	√x2+1		2x   √x2+1−x*   2√x2+1
=		*		=
	√x2+1−x2		(x2+1)

	√x2+1		(x2+1−x2		1
=		*		=
	1		(x2+1)*√x2+1		x2+1

	1		1
f'(x)=		−		=0
	x2+1		x2+1

stozek: to wtedy zostaje jeszcze pochodna arctg x co nie?

stozek: aha sory nie zauwazylem tego co w ostatenij linijce zrobilas, dzieki za pomoc

Mila: stożek jutro, Dobranoc.

stozek: i jak z tym stozkiem?

Jerzy:

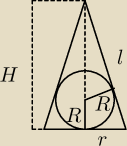
l		H − R		(H−R)*r
	=		⇔ l =
r		R		R

l² = H² + r²

(H − R)2r2		HR2
	= H2 + r2 ⇒ r2 =
R2		H −R

	1		H2R2
V =		π		.... i liczysz minimum
	3		H − 2R

wynik: H = 4R

Jerzy:

	HR2
trzecia linijka: r2 =
	H − 2R

stozek:

	1		H2R2
mam obliczyć minimum z V=		π		czyli pochodną z tego wyrażenia po prawej tak?
	3		H−2R

Jerzy: dokładnie tak

stozek:

	2H22R−4H2R2+H2R2
wychodzi mi coś w stylu		, da się to jakoś przekształcić do
	H2−4HR+4R2

H=4R czy od nowa liczyć pochodną?

Jerzy: ile wynosi pochodna z: H²R² ( gdzie R² to stała ) ?

stozek: pochodna ze stałej to 0 zawsze chyba nie? to to całe wyrażenie by było 0? wtedy reszta by nie miała sensu, to R² zostawiam i pochodna z tego H²R² to będzie 2HR²?

Jerzy: tak ... stałą sie wyłacza przed pochodną

	2HR2(H − 2R) − H2R2
V'(H) =		.... teraz uprządkuj licznik
	(H − 2R)2

(mianownika nie ruszaj)

Jerzy:

	1
oczywiście przed całością ma być:		π
	3

stozek: H²R²−2HR³?

stozek: i mianownik oczywiście na dole, sam licznik napisałem

Jerzy: przecież to pochodna ilorazu ... uporządkuj licznik ( drugi człon źle) , mianownik bez zmian

stozek: uporządkowałem licznik, tam nie liczyłem żadnej pochodnej: 2HR²(H−2R)−H²R²=2H²R²−4HR³−H²R²=H²R²−4HR³ gdzie mam błąd tutaj?

Jerzy: teraz już nie ( przedtem tak) , teraz w liczniku wyłącz przed nawias: HR²

stozek: HR²(H−4R)

Jerzy: dobra , teraz zapisz porządnie całą pochodną

stozek:

1		HR2(H−4R)
	π*
3		(H−2R)2

Jerzy: OK ... kiedy ta pochodna się zeruje ?

stozek: kiedy licznik jest równy zero czyli HR²=0 lub (H−4R)=0?

Jerzy: H = 0 ( odpada, bo nie ma stożka ) , H − 4R = 0 ⇔ H = 4R a więc tyumoże być ekstremum ( i jest ) ... skąd wiadomo,że to minimum ?

stozek: bo jakby R było większe to znak byłby ujemny czy coś w tym stylu? nie wiem, strzelam

Jerzy: nie ...warunkiem istnienia ekstremum jest zmiana znaku pochodnej w punkcie jej zerowania się , tutaj pochodna zmienia znak w punkcie: H = 4R z ujemnego na dodatni, a więc funkcja przechodzi z malejącej w rosnącą , a więc osiaga minimum

stozek: właśnie o tym myślałem, ale źle to ująłem , dziękuję za pomoc

stozek: jeszcze jedno pytanie, jak przeszedłeś z tego:

(H−R)2r2
	=H2+r2
R2

do tego:

	HR2
r2=		?
	H−2R

Jerzy: nie chce mi się pisać .. .zwykłe przekształcenia ... powymnażaj, przenieś wyrazy zawierające r² na lewa stronę , wyłacz: r² przed nawias ...itd