Geometria Przestrzenna. Trudne. maxL: Geometria Przestrzenna. Trudne. Pole podstawy graniastosłupa prostego trójkątnego jest równe P. Przez krawędź podstawy tej bryły poprowadzono płaszczyznę która przecina przeciwległą krawędź boczną i jest nachylona do płaszczyzny podstawy pod kątem 45* Oblicz pole otrzymanego przekroju.

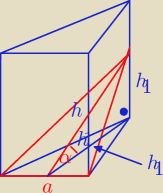
Janek191: α = 45^o

	2 P
P = 0,5 a*h1 ⇒ 2 P = a*h1 ⇒ a =
	h1

Z tw. Pitagorasa h = √2 h₁ więc

	2 P
Pp = 0, 5*a*h = 0,5 *		*√2 h1 = √2 P
	h1

Eta:

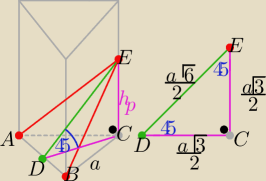
	a√3		a√3		a√6
|DC|=|CF|= hp=		|DE|=		*√2 =
	2		2		2

	1		a√6		a2√3
P(ABE)=		*a*		=		*√2= √2*P
	2		2		4

gdzie P −−− pole podstawy