geometria analityczna monia: Wyznacz wszystkie wartości parametru a (a Î R), dla których wektory u== [a² , 5a + 4] i v= [a – 1, –2] są prostopadłe. Dla najmniejszej wyznaczonej wartości parametru a napisz równanie prostej prostopadłej do wektora v−u i przechodzącej przez początek układu współrzędnych.

Mila: u^→= [a² , 5a + 4] i v^→= [a – 1, –2] u^→⊥v^→⇔ u^→ o v^→=0 u^→ o v^→=a²*(a−1)+(5a+4)*(−2)=0⇔ a³−a²−10a−8=0 W(1)=1−1−10−8≠0 W(2)=8−4−20+8≠0 W(−2)=−8−4+20−8=0⇔a=−2 jest pierwiastkiem wielomianu Schemat Hornera : a=−2 1 −1 −10 −8 1 −3 −4 0 a³−a²−10 a−8=(a+2)*(a²−3a−4) Δ=9+16=25

	3−5		3+5
a=		lub a=
	2		2

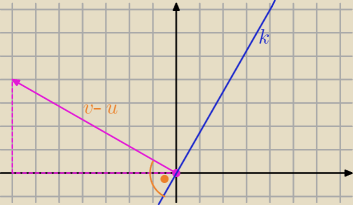
a=−1 lub a=4 −2<−1<4 u^→=[(−2)²,5*(−2)+4]=[4,−6] v^→=[−2−1,−2]=[−3,−2] v^→−u^→=[−3,−2]−[4,−6]=[−7,4] −7*(x−0)+4*(y−0)=0 k: −7x+4y=0 ==========