Okregi i wielokaty
5-latek:
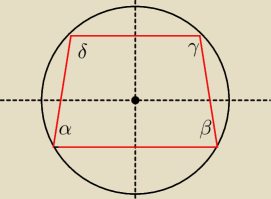
Cwiczenie nr 35 .
Udowodnij , ze trapez wpisany w okrag jest równoramienny
Wiem ze to jest prawda bo srodek okręgu opisanego na wielokącie lezy na na przecięciu
symetralnych wszystkich bokow wielokąta
Ale jak to zapisac ze katy ∡α+γ=360−(β+δ)
19 gru 22:54
5-latek:
Bo to chyba tak należy zapisac te kąty
19 gru 22:59
Jack:
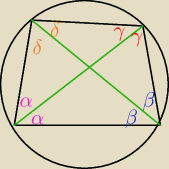
skoro jest wpisany w okrag to
2 α + 2 γ = 180
α + γ = 90
2 δ + 2 β = 180
δ + β = 90
2(α+β+γ+δ) = 360
α+β+γ+δ = 180
skoro
α + γ = 90 i δ + β = 90
α+γ = 180 − δ + β
19 gru 23:10
Jack: Poprawka do mojego :
α+γ = 180 − (δ + β)
Twoje :
Wlasciwie to co napisales "Ale jak to zapisac ze katy ∡α+γ=360−(β+δ)"
Skoro suma katow w czoworkacie jest 360
to
α+β+γ+δ = 360
czyli
α+γ = 360 − (β+γ)
19 gru 23:12
5-latek: O widzisz

19 gru 23:13
5-latek: Twój dowod bardziej mi się podoba

19 gru 23:14
Mila:
Dlaczego Jack masz tam dwusieczne ? To nie jest prawdą.
19 gru 23:47
5-latek: Milu 
Jeszcze raz się z Toba przywitam i podziekuje za zyczenia .

19 gru 23:56
Jack: Mila
To są przekątne trapezu

20 gru 00:03
piotr: Przecież przekątne trapezu dowolnego nie są jednocześnie dwusiecznymi kątów!
20 gru 00:07
Mila:
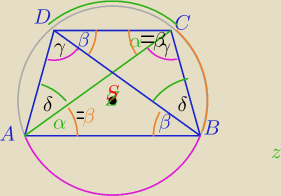
1) ABCD− trapez⇔
AB||DC i
|∡A|+|∡D|=180
o i |∡B|+|∡C|=180
o
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
∡CAB=∡CDB=α=β jako kąty wpisane oparte na tym samym
łuku
∡CBD=∡CAD=δ jako kąty wpisane oparte na tym samym
łuku
∡ADB=∡CAB=γ jako kąty wpisane oparte na tym samym
łuku⇔
|∡A|=|∡B|=α+δ
|∡D|=|∡C|=β+γ⇔Trapez jest równoramienny.
20 gru 00:13
Jack: tak, przeprszam, moglem zrobic z lukami ; /
20 gru 00:14
5-latek: Dziekuje Ci bardzo

20 gru 00:18
 Cwiczenie nr 35 .
Udowodnij , ze trapez wpisany w okrag jest równoramienny
Wiem ze to jest prawda bo srodek okręgu opisanego na wielokącie lezy na na przecięciu
symetralnych wszystkich bokow wielokąta
Ale jak to zapisac ze katy ∡α+γ=360−(β+δ)
Cwiczenie nr 35 .
Udowodnij , ze trapez wpisany w okrag jest równoramienny
Wiem ze to jest prawda bo srodek okręgu opisanego na wielokącie lezy na na przecięciu
symetralnych wszystkich bokow wielokąta
Ale jak to zapisac ze katy ∡α+γ=360−(β+δ)
 skoro jest wpisany w okrag to
2 α + 2 γ = 180
α + γ = 90
2 δ + 2 β = 180
δ + β = 90
2(α+β+γ+δ) = 360
α+β+γ+δ = 180
skoro
α + γ = 90 i δ + β = 90
α+γ = 180 − δ + β
skoro jest wpisany w okrag to
2 α + 2 γ = 180
α + γ = 90
2 δ + 2 β = 180
δ + β = 90
2(α+β+γ+δ) = 360
α+β+γ+δ = 180
skoro
α + γ = 90 i δ + β = 90
α+γ = 180 − δ + β


 Jeszcze raz się z Toba przywitam i podziekuje za zyczenia .
Jeszcze raz się z Toba przywitam i podziekuje za zyczenia .

 1) ABCD− trapez⇔
AB||DC i
|∡A|+|∡D|=180o i |∡B|+|∡C|=180o
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
∡CAB=∡CDB=α=β jako kąty wpisane oparte na tym samym łuku
∡CBD=∡CAD=δ jako kąty wpisane oparte na tym samym łuku
∡ADB=∡CAB=γ jako kąty wpisane oparte na tym samym łuku⇔
|∡A|=|∡B|=α+δ
|∡D|=|∡C|=β+γ⇔Trapez jest równoramienny.
1) ABCD− trapez⇔
AB||DC i
|∡A|+|∡D|=180o i |∡B|+|∡C|=180o
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
∡CAB=∡CDB=α=β jako kąty wpisane oparte na tym samym łuku
∡CBD=∡CAD=δ jako kąty wpisane oparte na tym samym łuku
∡ADB=∡CAB=γ jako kąty wpisane oparte na tym samym łuku⇔
|∡A|=|∡B|=α+δ
|∡D|=|∡C|=β+γ⇔Trapez jest równoramienny.
